Analyzing C4 A-Ci Curves

Overview

In this vignette, we will give an example showing how to analyze C₄A-C_i data using the PhotoGEA package. The commands in this vignette can be used to initialize your own script, as described in Customizing Your Script.

Background

Understanding C₄A-C_i Curves

An A-C_i curve (or CO₂ response curve) is a particular type of gas exchange measurement where a living leaf is exposed to varying concentrations of CO₂. For each CO₂ concentration in the sequence, the net assimilation rate ( $A_n$ ), stomatal conductance to H₂O ( $g_{sw}$ ), intercellular CO₂ concentration ( $C_i$ ), and other important quantities are measured and recorded. Typically, other environmental variables such as temperature, humidity, and incident photosynthetically-active photon flux density (PPFD) are held constant during the measurement sequence so that changes in photosynthesis can be attributed to CO₂ alone.

Because of their different cell structures and biochemical pathways, C₃ and C₄ plants have very different responses to CO₂. Here, we will only be discussing C₃ plants.

The full C₄ photosynthetic pathway is quite complicated, consisting of at least two hundred individual reactions, each of which may have an impact on a measured A-C_i curve. However, simplified models for photosynthesis are available and are much easier to understand and work with. These models tend to be based around PEP carboxylase and rubisco kinetics, describing how the net assimilation rate responds to the partial pressure of CO₂ in the mesophyll or bundle sheath cells. The most widely-used model is described in in Biochemical Models of Leaf Photosynthesis (S. von Caemmerer 2000).

This model provides a framework for understanding the changes in $A_n$ that occur as a C₄ plant is exposed to successively higher concentrations of CO₂. Overall, the photosynthetic response to CO₂ under high light conditions can be understood as follows:

For low levels of CO₂, CO₂ assimilation is primarily limited by PEP carboxylase activity in the mesophyll cells.
For higher levels of CO₂, CO₂ assimilation can be limited by Rubisco activity in the bundle sheath cells, PEP regeneration in the mesophyll cells, or light availability.

More specifically, the model provides equations that calculate the net assimilation rate $A_n$ from the maximumum rate of PEP carboxylation ( $V_{p,max}$ ), the maximum rate of Rubisco activity ( $V_{c,max}$ ), the maximum rate of PEP carboxylase regeneration ( $V_{p,r}$ ), the maximum electron transport rate ( $J_{max}$ ), the total rate of mitochondrial respiration across the mesophyll and bundle sheath cells ( $R_L$ ), the partial pressure of CO₂ in the mesophyll ( $P_{cm}$ ), and several other parameters. The full equations are quite complicated. $A_n$ is given by the smaller of the enzyme-limited rate ( $A_c$ ) and the light-limited rate ( $A_j$ ). $A_c$ is co-limited by PEP carboxylase activity, Rubisco activity, and PEP regeneration, while $A_j$ is co-limited by electron transport in the mesophyll and bundle-sheath cells. Under certain circumstances (when bundle sheath conductance is zero and all photosystem II activity occurs in the mesophyll), then the complicated equations reduce to a simpler situation where $A_n$ is given by the minimum of five separate rates:

The PEP-carboxylase-limited rate ( $A_{pc}$ )
The Rubisco-limited rate ( $A_r$ )
The PEP-regeneration-limited rate ( $A_{pr}$ )
The electron-transport-limited rate in the mesophyll ( $A_{jm}$ )
The electron-transport-limited rate in the bundle sheath ( $A_{jbs}$ )

The simplified version can be helpful for understanding the rough model behavior, but it is important to keep in mind that the real model is different, and that $A_n$ is generally not equal to the minimum of these five rates in the full model. The plot below shows an example of the full model output:

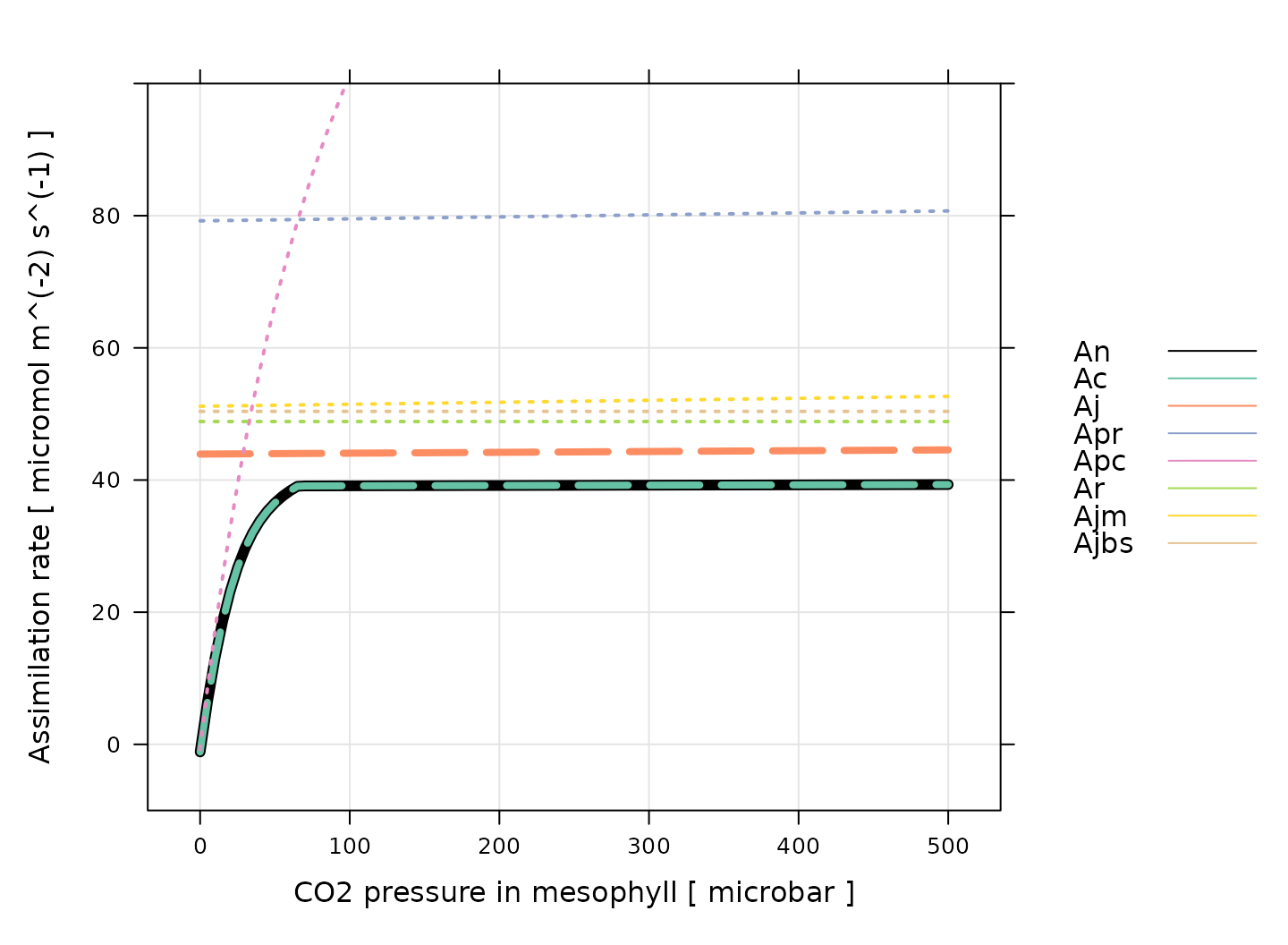
(Note: this figure was generated using the calculate_c4_assimilation function from the PhotoGEA package, and it represents the photosynethetic response of a C₄ leaf according to the model with RL_at_25 = 1 micromol m^(-2) s^(-1), Vpmax_at_25 = 150 micromol m^(-2) s^(-1), Vcmax_at_25 = 30 micromol m^(-2) s^(-1), Vpr = 80 micromol m^(-2) s^(-1), Jmax_at_opt = 400 micromol m^(-2) s^(-1), and a leaf temperature of 30 degrees C. Arrhenius temperature response parameters were taken from Susanne von Caemmerer (2021).)

There are several important things to notice about this plot:

For these conditions, $A_n$ is always equal to $A_c$ . Thus, assimilation is enzyme-limited across the entire range of CO₂ values.
The enzyme-limited rate $A_c$ is always smaller than either of the three rates related to individual enzymes ( $A_{pc}$ , $A_{pr}$ , and $A_r$ ).
The light-limited rate $A_j$ is always smaller than either of the two rates related to electron transport in individual cell types ( $A_{jm}$ and $A_{jb}$ ).
The dependence of $A_r$ , $A_j$ , and $A_{pr}$ on CO₂ concentration is very similar, where all three are nearly independent of CO₂.
The PEP-carboxylase-limited rate ( $A_{pc}$ ) is the only rate that approaches zero, which happens as the CO₂ concentration decreases.
Regardless of which process may be limiting assimilation, $A_n$ never decreases as CO₂ increases.

An important conclusion here is that PEP carboxylase always limits assimilation at low CO₂ concentrations, and that one or more of Rubisco activity, electron transport, and PEP regeneration limits assimilation at high CO₂ concentrations. These three processes each produce a plateau with a nearly flat response to CO₂.

One of the most common reasons to measure an A-C_i curve is to interpret it in the context of this model. In other words, by fitting the model’s equations to a measured curve, it is possible to estimate values for $R_L$ , $V_{pmax}$ , $V_{cmax}$ , $J_{max}$ , and others. See the documentation for calculate_c4_assimilation for more information about these important quantities.

From the discussion above, it is evident that determining the rate-limiting process at high $C_i$ in a C₄A-C_i curve is difficult or impossible because the three potentially limiting processes each exhibit nearly identical responses to CO₂. There are two main ways to deal with this issue:

One way is to assume a particular limiting process based on outside information. For example, curves measured under high light conditions (where electron transport rates will be high), and at warm temperatures (where PEP regeneration rates will be high) are likely to be Rubisco-limited at high $C_i$ .
Another option is to use an empirical non-rectangular hyperbola to fit the curve. This enables estimates of $V_{max}$ , the maximum rate of gross assimilation, which is related to the highest value of $A_n$ ( $A_{nmax}$ ) by $A_{nmax} = V_{max} - R_L$ . This quantity has no meaningful mechanistic interpretation but can be used to compare assimilation rates between groups of plants. When taking this approach, values of $V_{pmax}$ can still be estimated from the low $C_i$ part of the curve using the mechanistic model.

These approaches will be demonstrated below in this vignette.

Practicalities

There are a few other important practicalities to keep in mind when thinking about CO₂ response curves.

One point is that C₄ photosynthesis models generally predict the response of assimilation to the partial pressure of CO₂ in the mesophyll ( $P_{cm}$ ), but gas exchange measurements can only determine the CO₂ concentration in the leaf’s intercellular spaces ( $C_i$ ). Thus, an extra step is required when interpreting A-C_i curves. If the mesophyll conductance to CO₂ ( $g_{mc}$ ) and the total pressure ( $P$ ) are known, then it is possible to calculate values of $P_{cm}$ from $A_n$ , $C_i$ , $P$ , and $g_{mc}$ . Otherwise, it is also possible to assume an infinite mesophyll conductance; in this case, $C_m = C_i$ , and the estimated values of $V_{cmax}$ and other parameters can be considered to be “effective values” describing the plant’s response to intercellular CO₂.

Another important point is that plants generally do not appreciate being starved of CO₂, so it is not usually possible to start a response curve at low CO₂ and proceed upwards. A more typical approach is to:

Begin at ambient atmospheric CO₂ levels.
Decrease towards a low value.
Return to ambient levels and wait for the plant to reacclimate; this waiting period is usually accomplished by logging several points at ambient CO₂ levels.
Increase to higher values.

When taking this approach, it therefore becomes necessary to remove the extra points measured at ambient CO₂ levels and to reorder the points according to their CO₂ values before plotting or analyzing them.

The Data

A-C_i curves are commonly measured using a portable photosynthesis system such as the Licor Li-6800. These machines record values of $A_n$ , $g_{sw}$ , $C_i$ , and many other important quantities. They produce two types of output files: plain-text and Microsoft Excel. It is often more convenient to work with the Excel files since the entries can be easily modified (for example, to remove an extraneous row or add a new column). On the other hand, it can be more difficult to access the file contents using other pieces of software such as R. However, the PhotoGEA package reduces this barrier by including tools for reading Licor Excel files in R, which will be demonstrated in the following section.

Loading Packages

As always, the first step is to load the packages we will be using. In addition to PhotoGEA, we will also use the lattice package for generating plots.

# Load required packages
library(PhotoGEA)
library(lattice)

If the lattice package is not installed on your R setup, you can install it by typing install.packages('lattice').

Loading Licor Data

The PhotoGEA package includes two files representing A-C_i curves measured using two Li-6800 instruments. The data is stored in Microsoft Excel files, and includes curves measured from two different crop species (sorghum and maize) and several different plots of each. Each curve is a sixteen-point CO₂ response curve; in other words, the CO₂ concentration in the air surrounding the leaf was varied, and $A_n$ (among other variables) was measured at each CO₂ setpoint. Although these two files are based on real data, noise was added to it since it is unpublished, so these files should only be used as examples.

The files will be stored on your computer somewhere in your R package installation directory, and full paths to these files can be obtained with PhotoGEA_example_file_path:

# Define a vector of paths to the files we wish to load; in this case, we are
# loading example files included with the PhotoGEA package
file_paths <- c(
  PhotoGEA_example_file_path('c4_aci_1.xlsx'),
  PhotoGEA_example_file_path('c4_aci_2.xlsx')
)

(Note: When loading your own files for analysis, it is not advisable to use PhotoGEA_example_file_path as we have done here. Instead, file paths can be directly written, or files can be chosen using an interactive window. See Input Files below for more information.)

To actually read the data in the files and store them in R objects, we will use the read_gasex_file function from PhotoGEA. Since there are multiple files to read, we will call this function once for each file using lapply:

# Load each file, storing the result in a list
licor_exdf_list <- lapply(file_paths, function(fpath) {
  read_gasex_file(fpath, 'time')
})

The result from this command is an R list of “extended data frames” (abbreviated as exdf objects). The exdf class is a special data structure defined by the PhotoGEA package. In many ways, an exdf object is equivalent to a data frame, with the major difference being that an exdf object includes the units of each column. For more information, type ?exdf in the R terminal to access the built-in help menu entry, or check out the Working With Extended Data Frames vignette.

Generally, it is more convenient to work with a single exdf object rather than a list of them, so our next step will be to combine the objects in the list. This action can be accomplished using the rbind function, which combines table-like objects by their rows; in other words, it stacks two or more tables vertically. This action only makes sense if the tables have the same columns, so before we combine the exdf objects, we should make sure this is the case.

The PhotoGEA package includes a function called identify_common_columns that can be used to get the names of all columns that are present in all of the Licor files. Then, we can extract just those columns, and then combine the exdf objects into a single one.

# Get the names of all columns that are present in all of the Licor files
columns_to_keep <- do.call(identify_common_columns, licor_exdf_list)

# Extract just these columns
licor_exdf_list <- lapply(licor_exdf_list, function(x) {
  x[ , columns_to_keep, TRUE]
})

# Use `rbind` to combine all the data
licor_data <- do.call(rbind, licor_exdf_list)

Now we have a single R object called licor_data that includes all the data from several Licor Excel files. For more information about consolidating information from multiple files, see the Common Patterns section of the Working With Extended Data Frames vignette.

Validating the Data

Before attempting to fit the curves, it is a good idea to do some basic checks of the data to ensure it is organized properly and that it was measured properly.

Basic Checks

First, we should make sure there is a column in the data whose value uniquely identifies each curve. In this particular data set, several “user constants” were defined while making the measurements that help to identify each curve: instrument, species, and plot. However, neither of these columns alone are sufficient to uniquely identify each curve. We can solve this issue by creating a new column that combines the values from each of these:

# Create a new identifier column formatted like `instrument - species - plot`
licor_data[ , 'curve_identifier'] <-
  paste(licor_data[ , 'instrument'], '-', licor_data[ , 'species'], '-', licor_data[ , 'plot'])

The next step is to make sure that this column correctly identifies each response curve. To do this, we can use the check_response_curve_data function from PhotoGEA. Here we will supply the name of a column that should uniquely identify each response curve (curve_identifier), the expected number of points in each curve (16), the name of a “driving” column that should follow the same sequence in each curve (CO2_r_sp). If the data passes the checks, this function will have no output and will not produce any messages. (For more information, see the built-in help menu entry by typing ?check_response_curve_data.)

# Make sure the data meets basic requirements
check_response_curve_data(licor_data, 'curve_identifier', 16, 'CO2_r_sp')

However, if check_response_curve_data detects an issue, it will print a helpful message to the R terminal. For example, if we had specified the wrong number of points or the wrong identifier column, we would get error messages:

check_response_curve_data(licor_data, 'curve_identifier', 15)
#>      curve_identifier npts
#> 1   ripe1 - maize - 5   16
#> 2 ripe1 - sorghum - 2   16
#> 3 ripe1 - sorghum - 3   16
#> 4   ripe2 - maize - 2   16
#> 5 ripe2 - sorghum - 3   16
#> Error in check_response_curve_data(licor_data, "curve_identifier", 15): One or more curves does not have the expected number of points.

check_response_curve_data(licor_data, 'species', 16)
#>   species npts
#> 1   maize   32
#> 2 sorghum   48
#> Error in check_response_curve_data(licor_data, "species", 16): One or more curves does not have the expected number of points.

check_response_curve_data(licor_data, 'curve_identifier', 16, 'Ci')
#>  [1] "Point 1 from curve `ripe1 - maize - 5` has value `Ci = 95.1988547749169`, but the average value for this point across all curves is `Ci = 90.7350174923248`"   
#>  [2] "Point 1 from curve `ripe2 - maize - 2` has value `Ci = 112.053645568057`, but the average value for this point across all curves is `Ci = 90.7350174923248`"   
#>  [3] "Point 2 from curve `ripe2 - maize - 2` has value `Ci = 78.3677266731031`, but the average value for this point across all curves is `Ci = 73.7774387072254`"   
#>  [4] "Point 2 from curve `ripe2 - sorghum - 3` has value `Ci = 95.8971339710516`, but the average value for this point across all curves is `Ci = 73.7774387072254`" 
#>  [5] "Point 3 from curve `ripe2 - maize - 2` has value `Ci = 55.8461667809225`, but the average value for this point across all curves is `Ci = 50.2351057212952`"   
#>  [6] "Point 3 from curve `ripe2 - sorghum - 3` has value `Ci = 54.2879832747398`, but the average value for this point across all curves is `Ci = 50.2351057212952`" 
#>  [7] "Point 4 from curve `ripe2 - maize - 2` has value `Ci = 36.3299652323122`, but the average value for this point across all curves is `Ci = 34.7296260746293`"   
#>  [8] "Point 4 from curve `ripe2 - sorghum - 3` has value `Ci = 45.4786162389747`, but the average value for this point across all curves is `Ci = 34.7296260746293`" 
#>  [9] "Point 5 from curve `ripe1 - sorghum - 2` has value `Ci = 24.3220793641472`, but the average value for this point across all curves is `Ci = 22.6366731891658`" 
#> [10] "Point 5 from curve `ripe2 - maize - 2` has value `Ci = 25.3526198153885`, but the average value for this point across all curves is `Ci = 22.6366731891658`"   
#> [11] "Point 5 from curve `ripe2 - sorghum - 3` has value `Ci = 26.5962217290156`, but the average value for this point across all curves is `Ci = 22.6366731891658`" 
#> [12] "Point 6 from curve `ripe2 - sorghum - 3` has value `Ci = 20.6924342276327`, but the average value for this point across all curves is `Ci = 18.2682597489262`" 
#> [13] "Point 7 from curve `ripe1 - sorghum - 2` has value `Ci = 13.0676593944446`, but the average value for this point across all curves is `Ci = 11.7476810069077`" 
#> [14] "Point 7 from curve `ripe2 - maize - 2` has value `Ci = 14.0971182401318`, but the average value for this point across all curves is `Ci = 11.7476810069077`"   
#> [15] "Point 9 from curve `ripe1 - maize - 5` has value `Ci = 163.508148863318`, but the average value for this point across all curves is `Ci = 159.390938891699`"   
#> [16] "Point 9 from curve `ripe1 - sorghum - 3` has value `Ci = 174.479049333262`, but the average value for this point across all curves is `Ci = 159.390938891699`" 
#> [17] "Point 9 from curve `ripe2 - maize - 2` has value `Ci = 170.055243344855`, but the average value for this point across all curves is `Ci = 159.390938891699`"   
#> [18] "Point 10 from curve `ripe1 - maize - 5` has value `Ci = 147.168363231333`, but the average value for this point across all curves is `Ci = 134.474388889858`"  
#> [19] "Point 10 from curve `ripe2 - maize - 2` has value `Ci = 151.178147014491`, but the average value for this point across all curves is `Ci = 134.474388889858`"  
#> [20] "Point 10 from curve `ripe2 - sorghum - 3` has value `Ci = 147.942853301254`, but the average value for this point across all curves is `Ci = 134.474388889858`"
#> [21] "Point 11 from curve `ripe1 - maize - 5` has value `Ci = 301.610571803461`, but the average value for this point across all curves is `Ci = 295.553484685722`"  
#> [22] "Point 11 from curve `ripe1 - sorghum - 2` has value `Ci = 304.484438603537`, but the average value for this point across all curves is `Ci = 295.553484685722`"
#> [23] "Point 11 from curve `ripe2 - maize - 2` has value `Ci = 314.766889542375`, but the average value for this point across all curves is `Ci = 295.553484685722`"  
#> [24] "Point 11 from curve `ripe2 - sorghum - 3` has value `Ci = 300.976260955957`, but the average value for this point across all curves is `Ci = 295.553484685722`"
#> [25] "Point 12 from curve `ripe2 - maize - 2` has value `Ci = 511.309867405833`, but the average value for this point across all curves is `Ci = 469.330015405697`"  
#> [26] "Point 12 from curve `ripe2 - sorghum - 3` has value `Ci = 518.713451150252`, but the average value for this point across all curves is `Ci = 469.330015405697`"
#> [27] "Point 13 from curve `ripe2 - maize - 2` has value `Ci = 706.802465420149`, but the average value for this point across all curves is `Ci = 621.735292472354`"  
#> [28] "Point 13 from curve `ripe2 - sorghum - 3` has value `Ci = 684.288635299733`, but the average value for this point across all curves is `Ci = 621.735292472354`"
#> [29] "Point 14 from curve `ripe1 - sorghum - 2` has value `Ci = 788.919450361277`, but the average value for this point across all curves is `Ci = 771.269382813732`"
#> [30] "Point 14 from curve `ripe2 - maize - 2` has value `Ci = 862.408987557924`, but the average value for this point across all curves is `Ci = 771.269382813732`"  
#> [31] "Point 14 from curve `ripe2 - sorghum - 3` has value `Ci = 846.664713504987`, but the average value for this point across all curves is `Ci = 771.269382813732`"
#> [32] "Point 15 from curve `ripe1 - sorghum - 2` has value `Ci = 1019.63142264301`, but the average value for this point across all curves is `Ci = 980.559407812185`"
#> [33] "Point 15 from curve `ripe2 - maize - 2` has value `Ci = 1141.71338971252`, but the average value for this point across all curves is `Ci = 980.559407812185`"  
#> [34] "Point 15 from curve `ripe2 - sorghum - 3` has value `Ci = 1107.25473615995`, but the average value for this point across all curves is `Ci = 980.559407812185`"
#> [35] "Point 16 from curve `ripe1 - sorghum - 2` has value `Ci = 1468.33923855058`, but the average value for this point across all curves is `Ci = 1251.98886936329`"
#> [36] "Point 16 from curve `ripe2 - maize - 2` has value `Ci = 1381.01024312097`, but the average value for this point across all curves is `Ci = 1251.98886936329`"  
#> [37] "Point 16 from curve `ripe2 - sorghum - 3` has value `Ci = 1350.65791359197`, but the average value for this point across all curves is `Ci = 1251.98886936329`"
#> Error in check_response_curve_data(licor_data, "curve_identifier", 16, : The curves do not all follow the same sequence of the driving variable.

Plotting the A-C_i Curves

One qualitative way to check the data is to simply create a plot of the A-C_i curves. In this situation, the lattice library makes it simple to include each curve as its own separate subplot of a figure. For example:

# Plot all A-Ci curves in the data set
xyplot(
  A ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']'),
  ylab = paste('Net CO2 assimilation rate [', licor_data$units$A, ']')
)

Whoops! Why do these curves look so strange? Well, some of the issues are related to the sequence of CO₂ values that was used when measuring the curves. As discussed in Practicalities, there are several repeated points logged at the same CO₂ concentration, and the points are not logged in order of ascending or descending concentration. In fact, the sequence of CO₂ setpoints is as follows:

licor_data[licor_data[, 'curve_identifier'] == 'ripe2 - maize - 2', 'CO2_r_sp']
#>  [1]  400  300  200  150  100   75   50   20  400  400  600  800 1000 1200 1500
#> [16] 1800

Ideally, we would like to remove the ninth and tenth points (where the setpoint has been reset to 400 to allow the leaf to reacclimate to ambient CO₂ levels), and reorder the data so it is arranged from low to high values of Ci. This can be done using the organize_response_curve function from PhotoGEA:

# Remove points with duplicated `CO2_r_sp` values and order by `Ci`
licor_data <- organize_response_curve_data(
    licor_data,
    'curve_identifier',
    c(9, 10),
    'Ci'
)

Now we can plot them again:

# Plot all A-Ci curves in the data set
xyplot(
  A ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']'),
  ylab = paste('Net CO2 assimilation rate [', licor_data$units$A, ']')
)

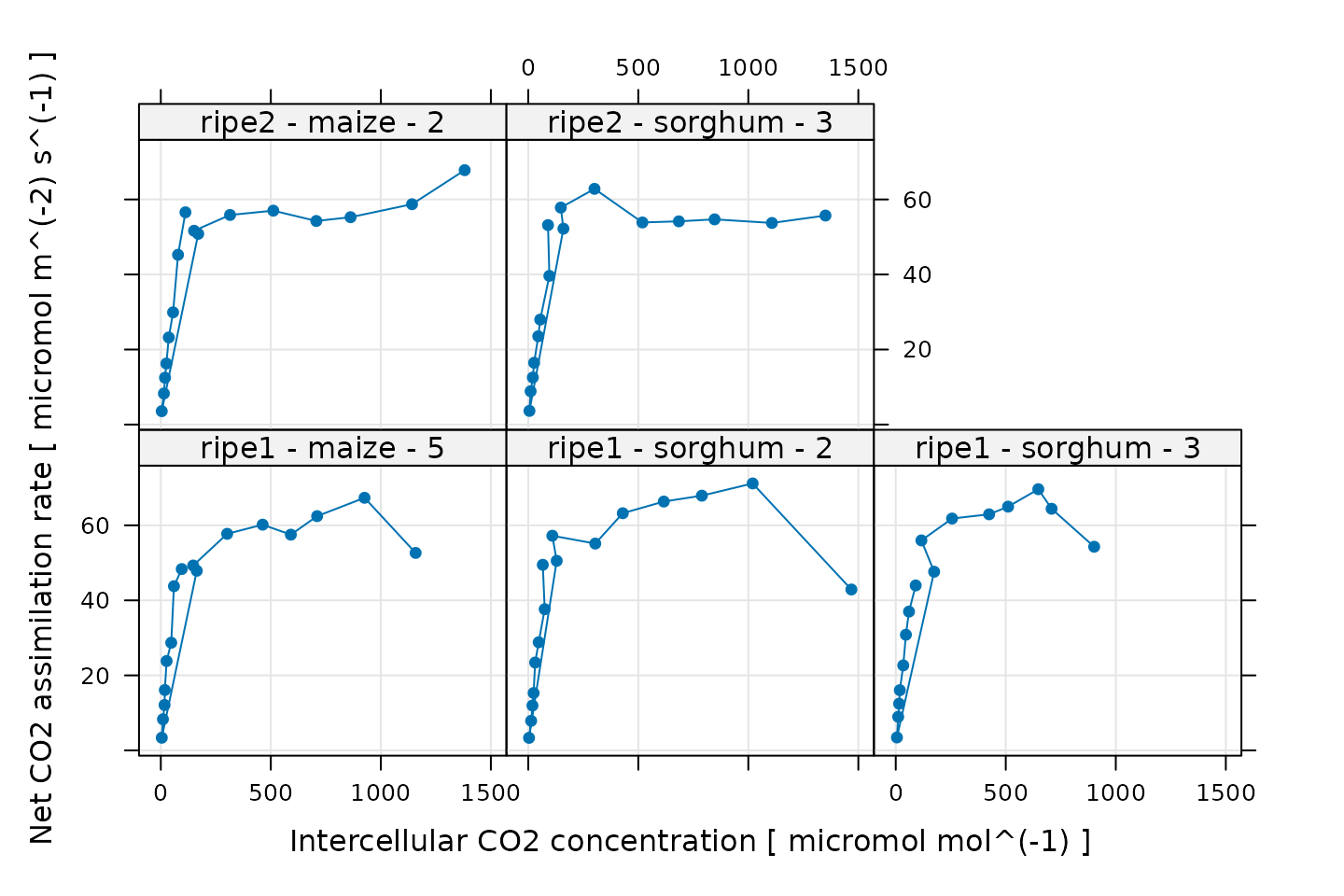
They still look a bit strange. Some of this is related to the noise that was intentionally added to the data. Nevertheless, there are a few points that we should probably exclude before attempting to fit the curves. One issue is that the model never predicts a decrease in $A$ when $Ci$ increases. So, it is usually a good idea to exclude any points at high $Ci$ where $A$ is observed to decrease by a large amount. This dropoff in assimilation is due to one or more processes that are not captured by the model, and the fits will be unreliable. We will remove these points later, after we have made several other data quality checks.

Additional Plots for Qualitative Validation

Sometimes a Licor will override the temperature or humidity controls while making measurements; in this case, conditions inside the measurement chamber may not be stable, and we may wish to exclude some of these points. We can check for these types of issues by making more plots. In the following sections, we will generate several different plots to check each curve for quality.

Humidity Control

# Make a plot to check humidity control
xyplot(
  RHcham + `Humidifier_%` + `Desiccant_%` ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  ylim = c(0, 100),
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']')
)

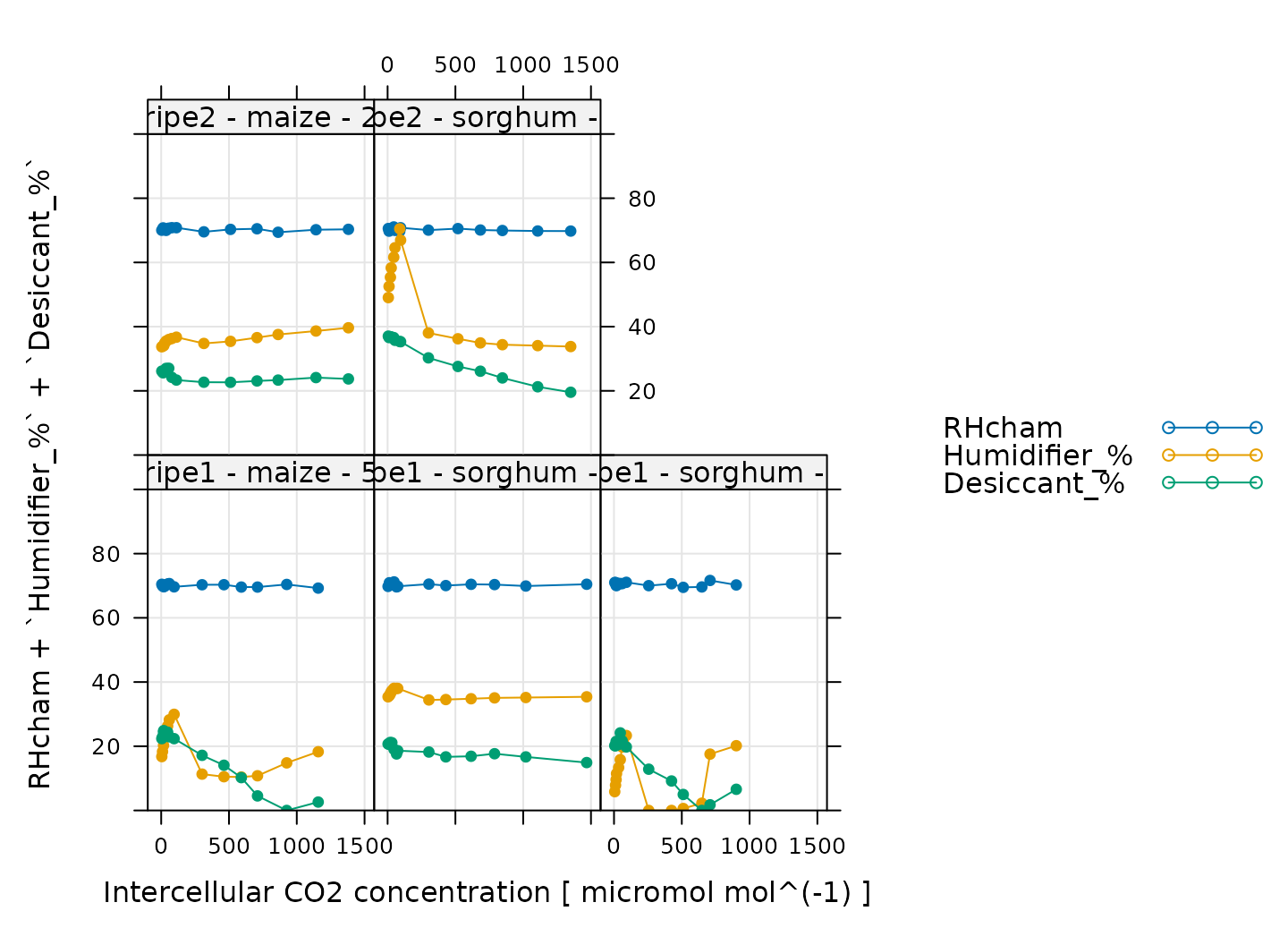
Here, Humidifier_% and Desiccant_% represent the flow from the humidifier and desiccant columns, where a value of 0 indicates that the valve to the column is fully closed and a value of 100 indicates that the valve to the column is fully opened. RHcham represents the relative humidity inside the chamber as a percentage (in other words, as a value between 0 and 100).

When these curves were measured, a chamber humidity setpoint was specified. So, when looking at this plot, we should check that the relative humidity is fairly constant during each curve. Typically, this should be accompanied by relatively smooth changes in the valve percentages as they accomodate changes in ambient humidity and leaf photosynthesis. In this plot, all the data looks good.

Temperature Control

# Make a plot to check temperature control
xyplot(
  TleafCnd + Txchg ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  ylim = c(25, 40),
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']'),
  ylab = paste0('Temperature (', licor_data$units$TleafCnd, ')')
)

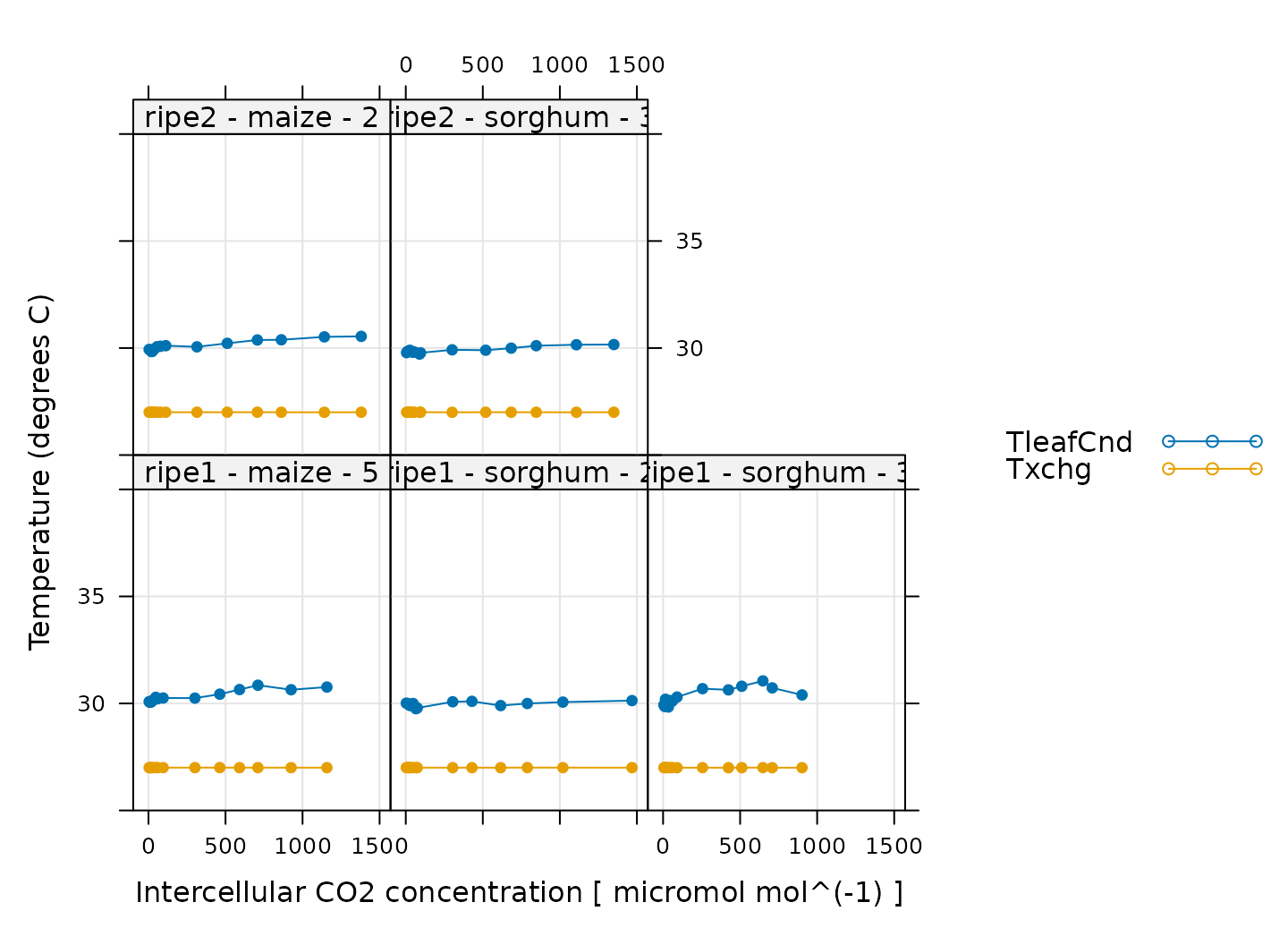
Here, TleafCnd is the leaf temperature measured using a thermocouple, and Txchg is the temperature of the heat exhanger that is used to control the air temperature in the measurement instrument. When these curves were measured, an exchanger setpoint was specified. So, when looking at this plot, we should check that Txchg is constant during each curve and that the leaf temperature does not vary in an erratic way. In this plot, all the data looks good.

CO₂ Control

# Make a plot to check CO2 control
xyplot(
  CO2_s + CO2_r + CO2_r_sp ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']'),
  ylab = paste0('CO2 concentration (', licor_data$units$CO2_r, ')')
)

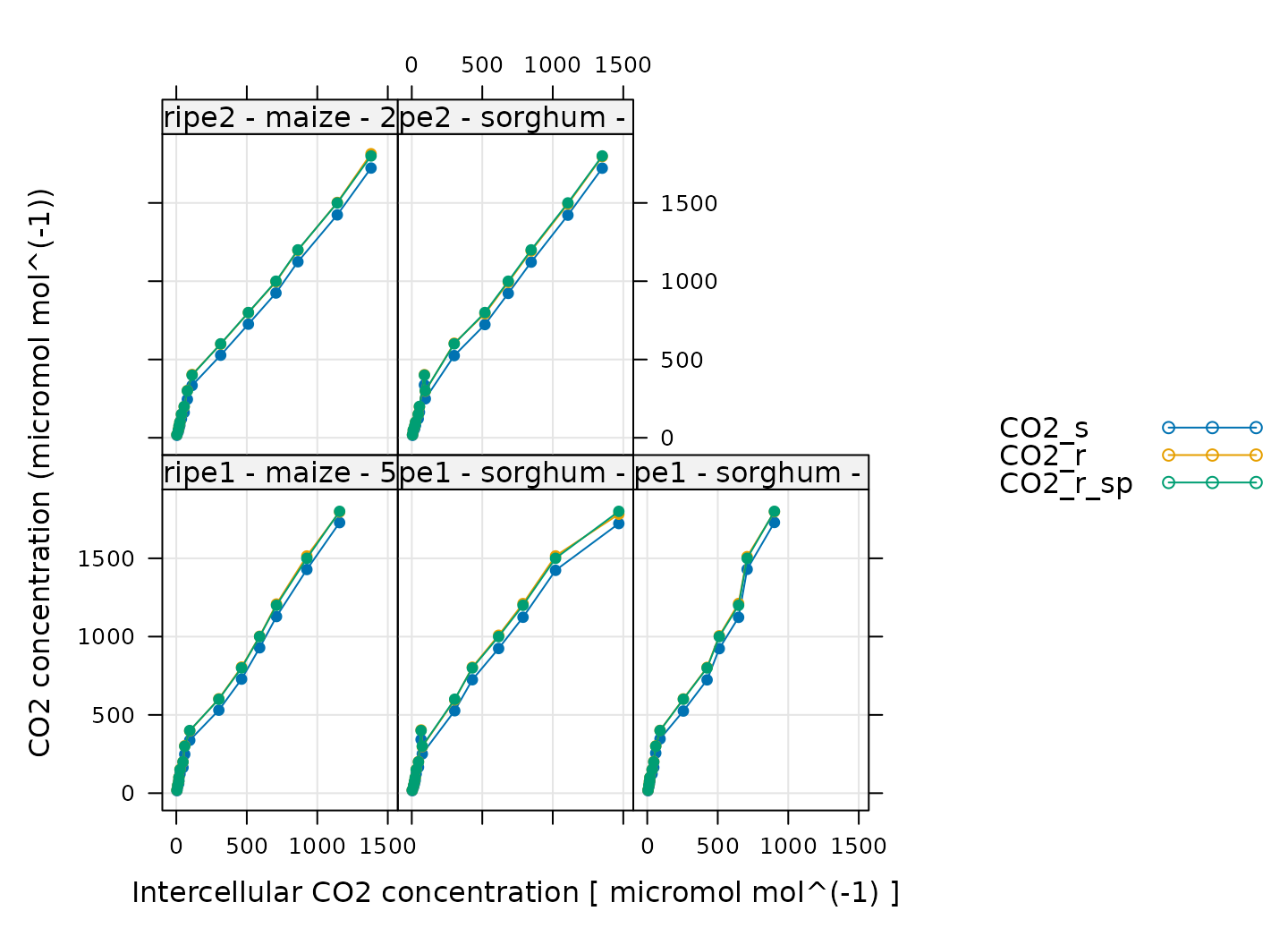
Here, CO2_s is the CO₂ concentration in the sample cell, CO2_r is the CO₂ concentration in the reference cell, and CO2_r_sp is the setpoint for CO2_r. When these curves were measured, a sequence of CO2_r values was specified, so, when looking at this plot, we should check that CO2_r is close to CO2_r_sp. We also expect that CO2_s should be a bit lower than CO2_r because the leaf in the sample chamber is assimilating CO₂, which should reduce its concentration in the surrounding air. (An exception to this rule occurs at very low values of CO2_r_sp, since in this case there is not enough carbon available to assimilate, and the leaf actually releases CO₂ due to respiration.) In this plot, all the data looks good.

Stability

# Make a plot to check stability criteria
xyplot(
  `A:OK` + `gsw:OK` + Stable ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']')
)

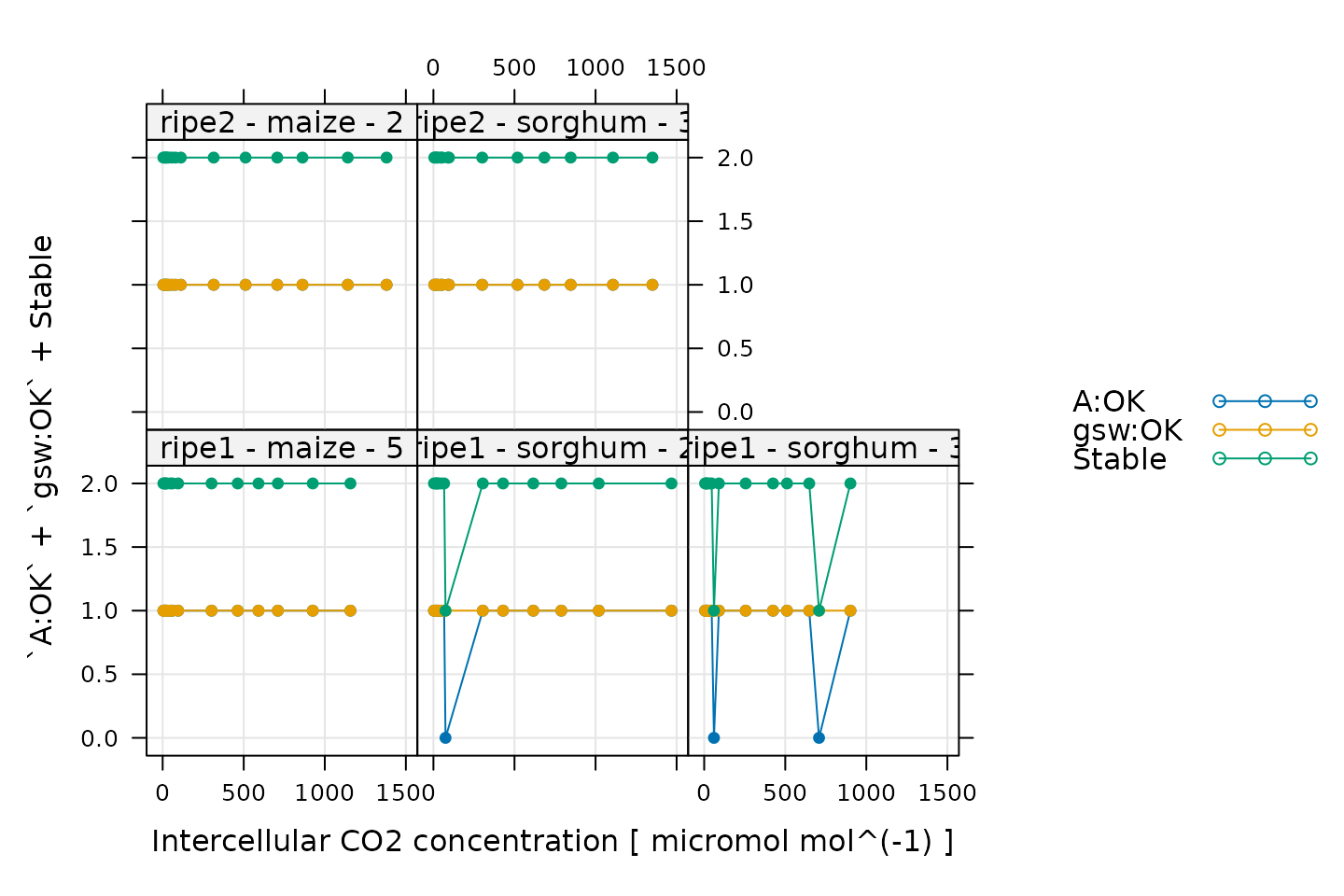
When measuring response curves with a Licor, it is possible to specify stability criteria for each point in addition to minimum and maximum wait times. In other words, once the set point for the driving variable is changed, the machine waits until the stability criteria are met; there is a minimum waiting period, and also a maximum to prevent the machine from waiting for too long.

When these curves were measured, stability criteria were supplied for the net assimilation rate A and the stomatal conductance gsw. The stability status for each was stored in the log file because the appropriate logging option for stability was set. Now, for each point, it is possible to check whether stability was achieved or whether the point was logged because the maximum waiting period had been met. If the maximum waiting period is reached and the plant has still not stabilized, the data point may be unreliable, so it can be helpful to check this information.

In the plot, A:OK indicates whether A was stable (0 for no, 1 for yes), gsw:OK indicates whether gsw was stable (0 for no, 1 for yes), and Stable indicates the total number of stability conditions that were met. So, we are looking for points where Stable is 2. Otherwise, we can check the other traces to see whether A or gsw was unstable.

Comparing these plots with the ones in Plotting the A-C_i Curves, it seems that none of the unstable points look particularly strange, so we will not remove them.

Cleaning the Licor Data

While checking over the plots in the previous sections, we noticed that some of the curves exhibit a sharp decrease in $A$ at high values of $C_i$ .

We can use the remove_points function from PhotoGEA to exclude these points. It just so happens that all of these points where $A_n$ suddenly decreases at high $C_i$ were measured by the ripe1 instrument and occur at the highest CO₂ setpoint value, so it is easy to specify them all at once.

# Remove points where `instrument` is `ripe1` and `CO2_r_sp` is 1800
licor_data <- remove_points(
  licor_data,
  list(instrument = 'ripe1', CO2_r_sp = 1800)
)

Fitting Licor Data

Now that we have checked the data quality, we are ready to perform the fitting. In order to fit the curves, there are several required pieces of information that are not included in the Licor data files as produced by the instrument: temperature-dependent values of important photosynthetic parameters such as $\gamma^*$ , values of the total pressure, and values of the partial pressure of CO₂ in the mesophyll $P_{cm}$ . However, the PhotoGEA package includes four functions to help with these calculations: calculate_arrhenius, calculate_peaked_gaussian, calculate_total_pressure, and apply_gm. Each of these requires an exdf object containing Licor data. The units for each required column will be checked in an attempt to avoid unit-related errors. More information about these functions can be obtained from the built-in help system by typing ?calculate_arrhenius, ?calculate_total_pressure, or ?apply_gm.

First, we can use calculate_arrhenius and calculate_peaked_gaussian:

# Calculate temperature-dependent values of C4 photosynthetic parameters
licor_data <- calculate_arrhenius(licor_data, c4_arrhenius_von_caemmerer)

licor_data <- calculate_peaked_gaussian(licor_data, c4_peaked_gaussian_von_caemmerer)

With these simple commands, we have used the leaf temperature from the Licor file to calculate values of several key C₄ photosynthetic parameters (Vcmax_norm, Vpmax_norm, RL_norm, Kc, Ko, Kp, gamma_star, ao, gmc and Jmax_norm) according to the temperature response parameters specified in Susanne von Caemmerer (2021). Notice that this command calculated values of the mesophyll conductance to CO2 (gmc) in units of mol m $^{-2}$ s $^{-1}$ bar $^{-1}$ . These values were estmated for Setaria viridis and may not be appropriate for all C₄ plants. Nevertheless, we will use them here.

Now we can use calculate_total_pressure and apply_gm to calculate PCm:

# Calculate the total pressure in the Licor chamber
licor_data <- calculate_total_pressure(licor_data)

# Calculate PCm
licor_data <- apply_gm(
  licor_data,
  'C4' # Indicate C4 photosynthesis
)

Together, these functions have added several new columns to licor_data, including gmc, PCm, gamma_star, and others. With this information, we are now ready to fit the curves.

Here we will demonstrate three different approaches to curve fitting. For these fits, we will be using the fit_c4_aci and fit_c4_aci_hyperbola functions from the PhotoGEA package, which each fit single response curves to estimate the values of key photosynthetic parameters.

To apply these functions to each curve in a larger data set and then consolidate the results, we can use them in conjunction with by and consolidate, which are also part of PhotoGEA. (For more information about these functions, see the built-in help menu entries by typing ?fit_c4_aci, ?fit_c4_aci_hyperbola, ?by.exdf, or ?consolidate, or check out the Common Patterns section of the Working With Extended Data Frames vignette.) Together, these functions will split apart the main data using the curve identifier column we defined before (Basic Checks), fit each A-C_i curve using the models discussed in Understanding C₄A-C_i Curves, and return the resulting parameters and fits.

For viewing the resulting fits, we will be using the plot_c4_aci_fit and plot_c4_aci_hyperbola_fit functions from PhotoGEA.

Mechanistic Fit, Assuming Rubisco Limitations

To ensure that the fitted assimilation rates are limited by Rubisco activity at high $C_i$ , we can set $V_{pr}$ and $J_{max}$ to extremely high values, which will ensure that PEP regeneration and light availability are never limiting. At the same time, we will allow $V_{cmax}$ to vary during the fit. This is the default behavior of fit_c4_aci, but here we will use the fit_options input argument to make it clear that we are requiring Rubisco limitations.

# The default optimizer uses randomness, so we will set a seed to ensure the
# results from this fit are always identical
set.seed(1234)

# Fit the C4 A-Ci curves with the mechanistic model, assuming Rubisco limitations
c4_aci_results_rubisco <- consolidate(by(
  licor_data,                       # The `exdf` object containing the curves
  licor_data[, 'curve_identifier'], # A factor used to split `licor_data` into chunks
  fit_c4_aci,                       # The function to apply to each chunk of `licor_data`
  Ca_atmospheric = 420,             # Used to estimate the operating point
  fit_options = list(Vcmax_at_25 = 'fit', Vpr = 1000, Jmax_at_opt = 1000)
))

Having made the fits, we can view the results:

# Plot the C4 A-Ci fits that were made assuming Rubisco limitations
plot_c4_aci_fit(
  c4_aci_results_rubisco,
  'curve_identifier',
  'Ci',
  ylim = c(-10, 100),
  main = 'Mechanistic fits assuming Rubisco limitations'
)

Overall, these fits look good. Note that because Rubisco activity and PEP carboxylase activity co-limit the net assimilation rate, $A_n$ is always smaller than either $A_r$ or $A_{pc}$ in these results.

Mechanistic Fit, Assuming Light Limitations

To ensure that the fitted assimilation rates are limited by light at high $C_i$ , we can set $V_{pr}$ and $V_{cmax}$ to extremely high values, which will ensure that PEP regeneration and Rubisco activity are never limiting. At the same time, we will allow $J_{max}$ to vary during the fit. This can be done using the fit_options input argument to fit_c4_aci.

# The default optimizer uses randomness, so we will set a seed to ensure the
# results from this fit are always identical
set.seed(1234)

# Fit the C4 A-Ci curves with the mechanistic model, assuming light limitations
c4_aci_results_light <- consolidate(by(
  licor_data,                       # The `exdf` object containing the curves
  licor_data[, 'curve_identifier'], # A factor used to split `licor_data` into chunks
  fit_c4_aci,                       # The function to apply to each chunk of `licor_data`
  Ca_atmospheric = 420,             # Used to estimate the operating point
  fit_options = list(Vcmax_at_25 = 1000, Vpr = 1000, Jmax_at_opt = 'fit')
))

Having made the fits, we can view the results:

# Plot the C4 A-Ci fits that were made assuming Rubisco limitations
plot_c4_aci_fit(
  c4_aci_results_light,
  'curve_identifier',
  'Ci',
  ylim = c(-10, 100),
  main = 'Mechanistic fits assuming light limitations'
)

Overall, these fits look good. Note that because electron transport and PEP carboxylase are independent in the model, there is a sharp transition from $A_n = A_{pc}$ to $A_n = A_j$ in these fits, in contrast to the Rubisco fits above, where there is a smooth transition between limiting states.

Semi-Empirical Fit

We can also take an empirical approach to curve fitting, where we use a non-rectangular hyperbola instead of the mechanistic model.

# The default optimizer uses randomness, so we will set a seed to ensure the
# results from this fit are always identical
set.seed(1234)

# Fit the C4 A-Ci curves with the empirical model
c4_aci_results_hyperbola <- consolidate(by(
  licor_data,                       # The `exdf` object containing the curves
  licor_data[, 'curve_identifier'], # A factor used to split `licor_data` into chunks
  fit_c4_aci_hyperbola              # The function to apply to each chunk of `licor_data`
))

Having made the fits, we can view the results:

# Plot the C4 A-Ci fits that were made using the empirical model
plot_c4_aci_hyperbola_fit(
  c4_aci_results_hyperbola,
  'curve_identifier',
  ylim = c(-10, 100),
  main = 'Empirical fits using a hyperbola'
)

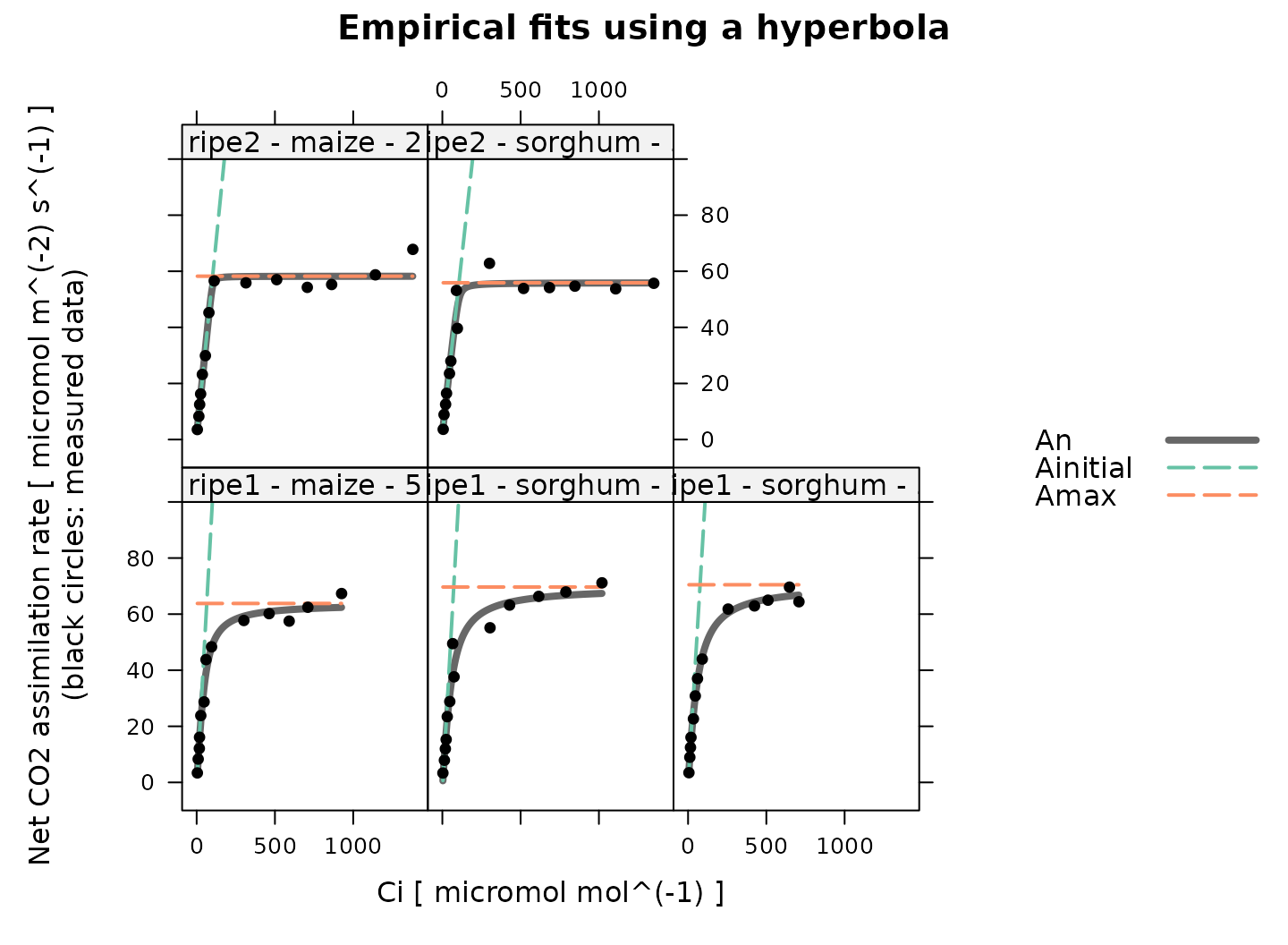
The hyperbola is used to estimate $V_{max}$ , which characterizes the maximum gross assimilation rate that occurs at high $C_i$ , such that $A_{max} = V_{max} - R_L$ is the highest net assimilation rate. It is common to pair this with an estimate $V_{pmax}$ made by fitting a mechanistic equation to the low- $C_i$ part of the curve:

$A_n = \frac{V_{pmax} \cdot C_i}{C_i + K_p} - R_L$

The full mechanistic model reduces to this particular equation when the following conditions are met:

The bundle sheath conductance ( $g_{bs}$ ) is zero.
No photosystem II activity occurs in the bundle sheath ( $\alpha_{PSII} = 0$ ).
The CO₂ concentration in the mesophyll is identical to the intercellular CO₂ concentration. This is the case when mesophyll conductance is infinitely large.

Here we will fit this equation to just the measured points where $C_i$ is below 60 ppm. To do this, we will also need to recalculate $PCm$ using an infinite value of mesophyll conductance.

# Get a subset of the data where Ci is below the threshold value
licor_data_low_ci <- licor_data[licor_data[, 'Ci'] <= 60, , TRUE]

# Set mesophyll conductance to infinity
licor_data_low_ci[, 'gmc'] <- Inf

# Recalculate PCm after changing mesophyll conductance
licor_data_low_ci <- apply_gm(
  licor_data_low_ci,
  'C4' # Indicate C4 photosynthesis
)

# The default optimizer uses randomness, so we will set a seed to ensure the
# results from this fit are always identical
set.seed(1234)

# Fit the C4 A-Ci curves with the mechanistic Vpmax equation
c4_aci_results_vpmax <- consolidate(by(
  licor_data_low_ci,                       # The `exdf` object containing the curves
  licor_data_low_ci[, 'curve_identifier'], # A factor used to split `licor_data` into chunks
  fit_c4_aci,                              # The function to apply to each chunk of `licor_data`
  fit_options = list(
    Vcmax_at_25 = 1000,
    Vpr = 1000,
    Jmax_at_opt = 1000,
    alpha_psii = 0,
    gbs = 0
  )
))

Having made the fits, we can view the results:

# Plot the C4 A-Ci fits that were made to the low Ci part of the curves
plot_c4_aci_fit(
  c4_aci_results_vpmax,
  'curve_identifier',
  'Ci',
  ylim = c(-10, 60),
  main = 'Mechanistic fits to the low Ci part of each curve'
)

Examining the Results

Accessing Best-Fit Estimates and Confidence Intervals

Each fit returns best-fit values and confidence limits for each parameter, which are stored in parameters element of the output list, another exdf object. These values can be viewed directly from R. For example, we can look at the estimated $V_{pmax}$ values from each mechanistic fit as follows:

# Specify columns to view
vpmax_columns <- c(
  'curve_identifier',
  'Vpmax_at_25_lower',
  'Vpmax_at_25',
  'Vpmax_at_25_upper'
)

# View Vpmax values from the mechanistic fit that assumed Rubisco limitations
c4_aci_results_rubisco$parameters[, vpmax_columns]
#>      curve_identifier Vpmax_at_25_lower Vpmax_at_25 Vpmax_at_25_upper
#> 1   ripe1 - maize - 5          133.8529    158.2040          187.1139
#> 2 ripe1 - sorghum - 2          123.4999    149.4453          179.5492
#> 3 ripe1 - sorghum - 3          115.9223    124.2466          133.2167
#> 4   ripe2 - maize - 2          135.7686    154.8675          176.9160
#> 5 ripe2 - sorghum - 3          110.0679    131.1353          156.6364

# View Vpmax values from the mechanistic fit that assumed light limitations
c4_aci_results_light$parameters[, vpmax_columns]
#>      curve_identifier Vpmax_at_25_lower Vpmax_at_25 Vpmax_at_25_upper
#> 1   ripe1 - maize - 5          76.83576    90.42360         109.79465
#> 2 ripe1 - sorghum - 2          85.68564   104.57110         123.45742
#> 3 ripe1 - sorghum - 3          75.85697    83.65982          91.46284
#> 4   ripe2 - maize - 2          91.95957    99.19943         108.64168
#> 5 ripe2 - sorghum - 3          74.14162    85.45425          96.76730

# View Vpmax values from the mechanistic fit to the low-Ci part of the curves
c4_aci_results_vpmax$parameters[, vpmax_columns]
#>      curve_identifier Vpmax_at_25_lower Vpmax_at_25 Vpmax_at_25_upper
#> 1   ripe1 - maize - 5          75.32530    82.31016          89.29504
#> 2 ripe1 - sorghum - 2          65.23357    70.17602          75.11849
#> 3 ripe1 - sorghum - 3          70.41548    73.30350          76.19152
#> 4   ripe2 - maize - 2          62.10453    64.47364          66.84276
#> 5 ripe2 - sorghum - 3          55.37449    57.38421          59.39391

Here we can see that the estimates made from the mechanistic fit with Rubisco limitations are generally the largest, while those made from just the low- $C_i$ points are the lowest.

Estimates of other parameters, such as $V_{cmax}$ , $J_{max}$ , $V_{max}$ , and $R_L$ can be accessed with similar commands.

Visualizing Average Best-Fit Parameters

We can also visualize the best-fit parameters using plots. One way to do this is by using the barchart_with_errorbars function from PhotoGEA to create barcharts of the average values for each species. This function will ignore any NA values from curves where a parameter could not be reliably estimated, and the error bars will show the standard error of the mean for each species. Here we will take a look at the $V_{cmax}$ estimates.

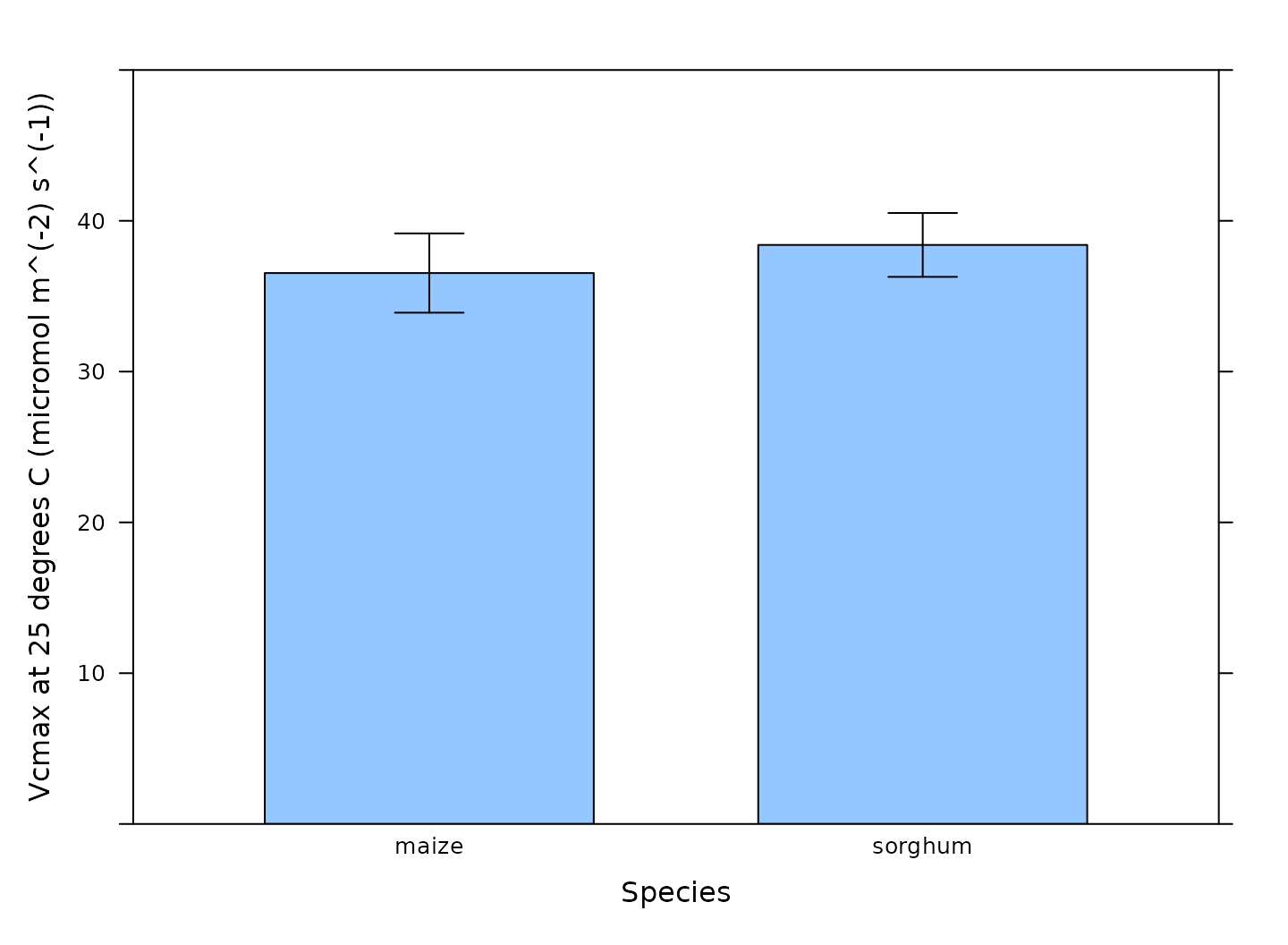
# Make a barchart showing average Vcmax values
barchart_with_errorbars(
  c4_aci_results_rubisco$parameters[, 'Vcmax_at_25'],
  c4_aci_results_rubisco$parameters[, 'species'],
  ylim = c(0, 50),
  xlab = 'Species',
  ylab = paste0('Vcmax at 25 degrees C (', c4_aci_results_rubisco$parameters$units$Vcmax_at_25, ')')
)

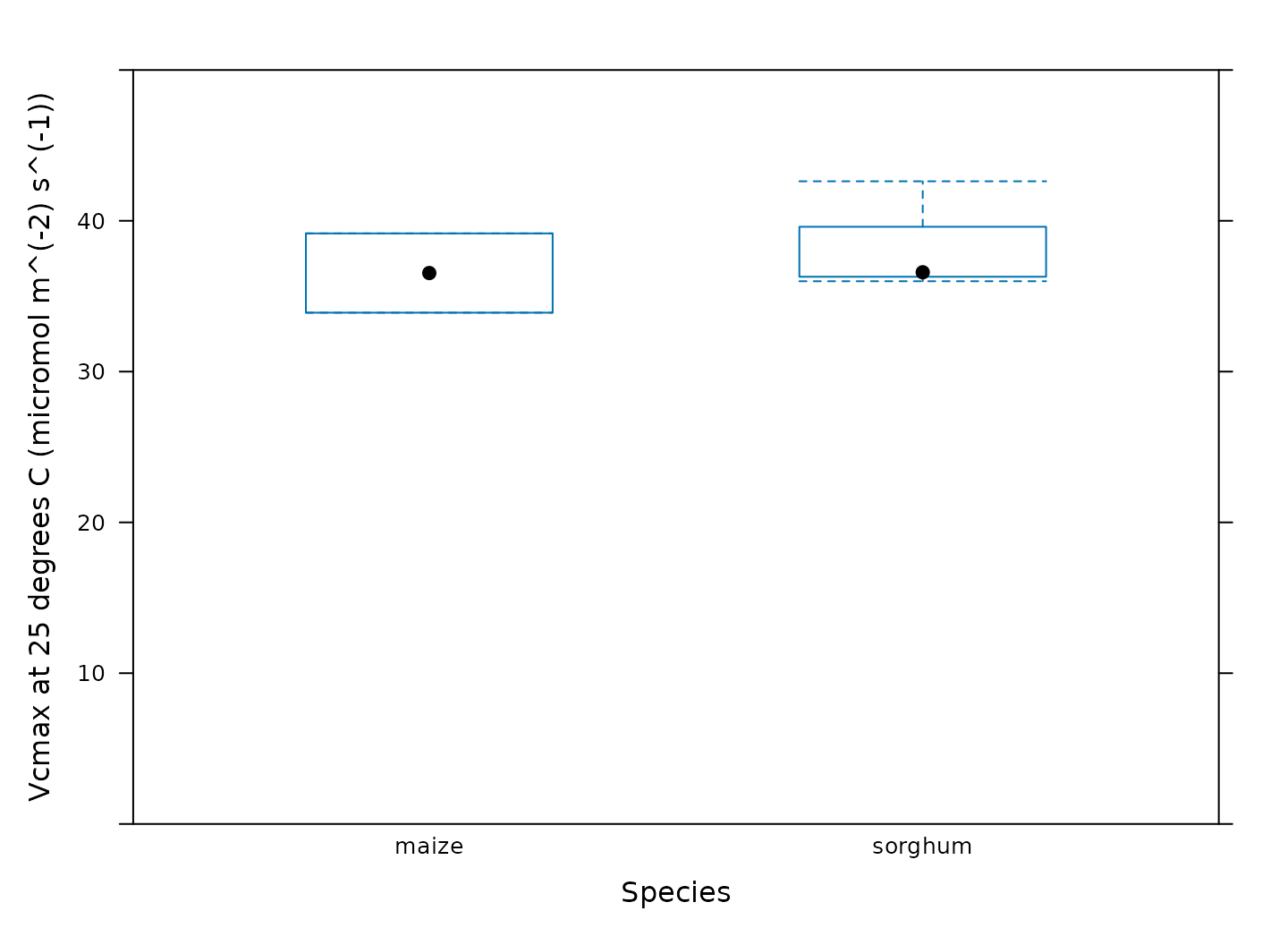
Another option is to create box-whisper plots using the bwplot function from the lattice package:

# Make a boxplot showing the distribution of Vcmax values
bwplot(
  Vcmax_at_25 ~ species,
  data = c4_aci_results_rubisco$parameters$main_data,
  ylim = c(0, 50),
  xlab = 'Species',
  ylab = paste0('Vcmax at 25 degrees C (', c4_aci_results_rubisco$parameters$units$Vcmax_at_25, ')')
)

Calculating Average Best-Fit Parameters

We can also calculate average values and standard errors of the best-fit parameters for each species using the basic_stats function from PhotoGEA:

# Compute the average and standard error of each parameter for each species
# from one of the mechanistic fits
c4_aci_averages_rubisco <- basic_stats(c4_aci_results_rubisco$parameters, 'species')

# View the averages and errors
columns_to_view <- c(
  'species',
  'Vcmax_at_25_avg', 'Vcmax_at_25_stderr',
  'Vpmax_at_25_avg', 'Vpmax_at_25_stderr',
  'RL_at_25_avg', 'RL_at_25_stderr'
)

c4_aci_averages_rubisco[ , columns_to_view]
#>   species Vcmax_at_25_avg Vcmax_at_25_stderr Vpmax_at_25_avg Vpmax_at_25_stderr
#> 1   maize        36.53579           2.628570        156.5358           1.668228
#> 2 sorghum        38.39997           2.117231        134.9424           7.519182
#>   RL_at_25_avg RL_at_25_stderr
#> 1   -0.1333101        2.842192
#> 2   -0.9351559        1.442296

Other Ideas for Synthesizing Results

Statistical tests to check for differences between groups can be performed within R using other packages such as onewaytests or DescTools. Alternatively, the parameter values can be exported to a comma-separated-value (CSV) file and analyzed in another software environment like jmp.

Customizing Your Script

Note that most of the commands in this vignette have been written in a general way so they can be used as the basis for your own analysis script (see Commands From This Document). In order to use them in your own script, some or all of the following changes may be required. There may also be others not specifically mentioned here.

Input Files

The file paths specified in file_paths will need to be modified so they point to your Licor files. One way to do this in your own script is to simply write out relative or absolute paths to the files you wish to load. For example, you could replace the previous definition of file_paths with this one:

# Define a vector of paths to the files we wish to load
file_paths <- c(
  'myfile1.xlsx',        # `myfile1.xlsx` must be in the current working directory
  'C:/documents/myfile2' # This is an absolute path to `myfile2`
)

You may also want to consider using the choose_input_licor_files function from PhotoGEA; this function will create a pop-up browser window where you can interactively select a set of files. Sometimes this is more convenient than writing out file paths or names. For example, you could replace the previous definition of file_paths with this one:

# Interactively define a vector of paths to the files we wish to load
file_paths <- choose_input_licor_files()

Unfortunately, choose_input_licor_files is only available in interactive R sessions running on Microsoft Windows, but there is also a platform-independent option: choose_input_files. See the Translation section of the Developing a Data Analysis Pipeline vignette for more details.

Curve Identifier

Depending on which user constants are defined in your Licor Excel files, you may need to modify the definition of the curve_identifier column.

Data Cleaning

Depending on the qualitative data checks, you may need to change the input arguments to remove_points. It might also not be necessary to remove the unstable points before performing the fits. Often, it is helpful to not perform any data cleaning at first, and then remove problematic points if they seem to cause problems with the fits.

Averages and Standard Errors

Depending on how your data is organized, you may want to change the column used to divide the data when calculating averages and standard errors.

Plots

You may need to change the axis limits in some or all of the plots. Alternatively, you can remove them, allowing xyplot to automatically choose them for you.

You may also want to consider using the pdf_print function from PhotoGEA to save some or all of your plots as PDFs. See the help page for more info: ?pdf_print.

Saving Results

You may want to use write.csv.exdf to save some or all of the fitting results as CSV files. When writing the contents of an exdf object to a CSV file, using write.csv.exdf rather than write.csv will ensure that units are included with each column.

For example, the following commands will save the results from one of the mechanistic fits, allowing you to interactively choose output filenames for the resulting CSV files:

write.csv.exdf(c4_aci_results_rubisco$fits, file.choose())
write.csv.exdf(c4_aci_results_rubisco$parameters, file.choose())
write.csv.exdf(c4_aci_averages_rubisco, file.choose())

Commands From This Document

The following code chunk includes all the central commands used throughout this document. They are compiled here to make them easy to copy/paste into a text file to initialize your own script. Annotation has also been added to clearly indicate the four steps involved in data analysis, as described in the Developing a Data Analysis Pipeline vignette.

###
### PRELIMINARIES:
### Loading packages, defining constants, creating helping functions, etc.
###

# Load required packages
library(PhotoGEA)
library(lattice)

###
### TRANSLATION:
### Creating convenient R objects from raw data files
###

## IMPORTANT: When loading your own files, it is not advised to use
## `PhotoGEA_example_file_path` as in the code below. Instead, write out the
## names or use the `choose_input_licor_files` function.

# Define a vector of paths to the files we wish to load; in this case, we are
# loading example files included with the PhotoGEA package
file_paths <- c(
  PhotoGEA_example_file_path('c4_aci_1.xlsx'),
  PhotoGEA_example_file_path('c4_aci_2.xlsx')
)

# Load each file, storing the result in a list
licor_exdf_list <- lapply(file_paths, function(fpath) {
  read_gasex_file(fpath, 'time')
})

# Get the names of all columns that are present in all of the Licor files
columns_to_keep <- do.call(identify_common_columns, licor_exdf_list)

# Extract just these columns
licor_exdf_list <- lapply(licor_exdf_list, function(x) {
  x[ , columns_to_keep, TRUE]
})

# Use `rbind` to combine all the data
licor_data <- do.call(rbind, licor_exdf_list)

###
### VALIDATION:
### Organizing the data, checking its consistency and quality, cleaning it
###

# Create a new identifier column formatted like `instrument - species - plot`
licor_data[ , 'curve_identifier'] <-
  paste(licor_data[ , 'instrument'], '-', licor_data[ , 'species'], '-', licor_data[ , 'plot'])

# Make sure the data meets basic requirements
check_response_curve_data(licor_data, 'curve_identifier', 16, 'CO2_r_sp')

# Remove points with duplicated `CO2_r_sp` values and order by `Ci`
licor_data <- organize_response_curve_data(
    licor_data,
    'curve_identifier',
    c(9, 10),
    'Ci'
)

# Plot all A-Ci curves in the data set
xyplot(
  A ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']'),
  ylab = paste('Net CO2 assimilation rate [', licor_data$units$A, ']')
)

# Make a plot to check humidity control
xyplot(
  RHcham + `Humidifier_%` + `Desiccant_%` ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  ylim = c(0, 100),
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']')
)

# Make a plot to check temperature control
xyplot(
  TleafCnd + Txchg ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  ylim = c(25, 40),
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']'),
  ylab = paste0('Temperature (', licor_data$units$TleafCnd, ')')
)

# Make a plot to check CO2 control
xyplot(
  CO2_s + CO2_r + CO2_r_sp ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']'),
  ylab = paste0('CO2 concentration (', licor_data$units$CO2_r, ')')
)

# Make a plot to check stability criteria
xyplot(
  `A:OK` + `gsw:OK` + Stable ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']')
)


# Remove points where `instrument` is `ripe1` and `CO2_r_sp` is 1800
licor_data <- remove_points(
  licor_data,
  list(instrument = 'ripe1', CO2_r_sp = 1800)
)

###
### PROCESSING:
### Extracting new pieces of information from the data
###

# Calculate temperature-dependent values of C4 photosynthetic parameters
licor_data <- calculate_arrhenius(licor_data, c4_arrhenius_von_caemmerer)

licor_data <- calculate_peaked_gaussian(licor_data, c4_peaked_gaussian_von_caemmerer)

# Calculate the total pressure in the Licor chamber
licor_data <- calculate_total_pressure(licor_data)

# Calculate PCm
licor_data <- apply_gm(
  licor_data,
  'C4' # Indicate C4 photosynthesis
)

##
## Mechanistic fits, assuming Rubisco limitations
##

# The default optimizer uses randomness, so we will set a seed to ensure the
# results from this fit are always identical
set.seed(1234)

# Fit the C4 A-Ci curves with the mechanistic model, assuming Rubisco limitations
c4_aci_results_rubisco <- consolidate(by(
  licor_data,                       # The `exdf` object containing the curves
  licor_data[, 'curve_identifier'], # A factor used to split `licor_data` into chunks
  fit_c4_aci,                       # The function to apply to each chunk of `licor_data`
  Ca_atmospheric = 420,             # Used to estimate the operating point
  fit_options = list(Vcmax_at_25 = 'fit', Vpr = 1000, Jmax_at_opt = 1000)
))

# Plot the C4 A-Ci fits that were made assuming Rubisco limitations
plot_c4_aci_fit(
  c4_aci_results_rubisco,
  'curve_identifier',
  'Ci',
  ylim = c(-10, 100),
  main = 'Mechanistic fits assuming Rubisco limitations'
)

##
## Mechanistic fits, assuming light limitations
##

# The default optimizer uses randomness, so we will set a seed to ensure the
# results from this fit are always identical
set.seed(1234)

# Fit the C4 A-Ci curves with the mechanistic model, assuming light limitations
c4_aci_results_light <- consolidate(by(
  licor_data,                       # The `exdf` object containing the curves
  licor_data[, 'curve_identifier'], # A factor used to split `licor_data` into chunks
  fit_c4_aci,                       # The function to apply to each chunk of `licor_data`
  Ca_atmospheric = 420,             # Used to estimate the operating point
  fit_options = list(Vcmax_at_25 = 1000, Vpr = 1000, Jmax_at_opt = 'fit')
))

# Plot the C4 A-Ci fits that were made assuming Rubisco limitations
plot_c4_aci_fit(
  c4_aci_results_light,
  'curve_identifier',
  'Ci',
  ylim = c(-10, 100),
  main = 'Mechanistic fits assuming light limitations'
)

##
## Semi-empirical fits
##

# The default optimizer uses randomness, so we will set a seed to ensure the
# results from this fit are always identical
set.seed(1234)

# Fit the C4 A-Ci curves with the empirical model
c4_aci_results_hyperbola <- consolidate(by(
  licor_data,                       # The `exdf` object containing the curves
  licor_data[, 'curve_identifier'], # A factor used to split `licor_data` into chunks
  fit_c4_aci_hyperbola              # The function to apply to each chunk of `licor_data`
))

# Plot the C4 A-Ci fits that were made using the empirical model
plot_c4_aci_hyperbola_fit(
  c4_aci_results_hyperbola,
  'curve_identifier',
  ylim = c(-10, 100),
  main = 'Empirical fits using a hyperbola'
)

# Get a subset of the data where Ci is below the threshold value
licor_data_low_ci <- licor_data[licor_data[, 'Ci'] <= 60, , TRUE]

# Set mesophyll conductance to infinity
licor_data_low_ci[, 'gmc'] <- Inf

# Recalculate PCm after changing mesophyll conductance
licor_data_low_ci <- apply_gm(
  licor_data_low_ci,
  'C4' # Indicate C4 photosynthesis
)

# The default optimizer uses randomness, so we will set a seed to ensure the
# results from this fit are always identical
set.seed(1234)

# Fit the C4 A-Ci curves with the mechanistic Vpmax equation
c4_aci_results_vpmax <- consolidate(by(
  licor_data_low_ci,                       # The `exdf` object containing the curves
  licor_data_low_ci[, 'curve_identifier'], # A factor used to split `licor_data` into chunks
  fit_c4_aci,                              # The function to apply to each chunk of `licor_data`
  fit_options = list(
    Vcmax_at_25 = 1000,
    Vpr = 1000,
    Jmax_at_opt = 1000,
    alpha_psii = 0,
    gbs = 0
  )
))

# Plot the C4 A-Ci fits that were made to the low Ci part of the curves
plot_c4_aci_fit(
  c4_aci_results_vpmax,
  'curve_identifier',
  'Ci',
  ylim = c(-10, 60),
  main = 'Mechanistic fits to the low Ci part of each curve'
)

###
### SYNTHESIS:
### Using plots and statistics to help draw conclusions from the data
###

# Make a barchart showing average Vcmax values
barchart_with_errorbars(
  c4_aci_results_rubisco$parameters[, 'Vcmax_at_25'],
  c4_aci_results_rubisco$parameters[, 'species'],
  ylim = c(0, 50),
  xlab = 'Species',
  ylab = paste0('Vcmax at 25 degrees C (', c4_aci_results_rubisco$parameters$units$Vcmax_at_25, ')')
)

# Make a boxplot showing the distribution of Vcmax values
bwplot(
  Vcmax_at_25 ~ species,
  data = c4_aci_results_rubisco$parameters$main_data,
  ylim = c(0, 50),
  xlab = 'Species',
  ylab = paste0('Vcmax at 25 degrees C (', c4_aci_results_rubisco$parameters$units$Vcmax_at_25, ')')
)

# Compute the average and standard error of each parameter for each species
# from one of the mechanistic fits
c4_aci_averages_rubisco <- basic_stats(c4_aci_results_rubisco$parameters, 'species')

# View the averages and errors
columns_to_view <- c(
  'species',
  'Vcmax_at_25_avg', 'Vcmax_at_25_stderr',
  'Vpmax_at_25_avg', 'Vpmax_at_25_stderr',
  'RL_at_25_avg', 'RL_at_25_stderr'
)

c4_aci_averages_rubisco[ , columns_to_view]

References

Caemmerer, S. von. 2000. Biochemical Models of Leaf Photosynthesis. CSIRO Publishing. https://doi.org/10.1071/9780643103405.

Caemmerer, Susanne von. 2021. “Updating the Steady-State Model of C4 Photosynthesis.” Journal of Experimental Botany 72 (17): 6003–17. https://doi.org/10.1093/jxb/erab266.

Overview

Background

Understanding C4A-Ci Curves

Practicalities

The Data

Loading Packages

Loading Licor Data

Validating the Data

Basic Checks

Plotting the A-Ci Curves

Additional Plots for Qualitative Validation

Humidity Control

Temperature Control

CO2 Control

Stability

Cleaning the Licor Data

Fitting Licor Data

Mechanistic Fit, Assuming Rubisco Limitations

Mechanistic Fit, Assuming Light Limitations

Semi-Empirical Fit

Examining the Results

Accessing Best-Fit Estimates and Confidence Intervals

Visualizing Average Best-Fit Parameters

Calculating Average Best-Fit Parameters

Other Ideas for Synthesizing Results

Customizing Your Script

Input Files

Curve Identifier

Data Cleaning

Averages and Standard Errors

Plots

Saving Results

Commands From This Document

References

Understanding C₄A-C_i Curves

Plotting the A-C_i Curves

CO₂ Control