Analyzing C3 A-Ci Curves

Overview

In this vignette, we will give an example showing how to analyze C₃A-C_i data using the PhotoGEA package. The commands in this vignette can be used to initialize your own script, as described in Customizing Your Script.

Background

Understanding C₃A-C_i Curves

An A-C_i curve (or CO₂ response curve) is a particular type of gas exchange measurement where a living leaf is exposed to varying concentrations of CO₂. For each CO₂ concentration in the sequence, the net assimilation rate ( $A_n$ ), stomatal conductance to H₂O ( $g_{sw}$ ), intercellular CO₂ concentration ( $C_i$ ), and other important quantities are measured and recorded. Typically, other environmental variables such as temperature, humidity, and incident photosynthetically-active photon flux density (PPFD) are held constant during the measurement sequence so that changes in photosynthesis can be attributed to CO₂ alone.

Because of their different cell structures and biochemical pathways, C₃ and C₄ plants have very different responses to CO₂. Here, we will only be discussing C₃ plants.

The full C₃ photosynthetic pathway is quite complicated, consisting of at least two hundred individual reactions, each of which may have an impact on a measured A-C_i curve. However, simplified models for photosynthesis are available and are much easier to understand and work with. These models tend to be based around Rubisco kinetics, describing how the net assimilation rate responds to the amount of CO₂ available in the chloroplast. The most widely-used model is typically referred to as the Farquhar-von-Caemmerer-Berry model (often shortened to the FvCB model or Farquhar model) after the three scientists who originally developed it. An excellent description of this model can be found in Biochemical Models of Leaf Photosynthesis (Caemmerer 2000), subject to a few additional considerations discussed Lochocki and McGrath (2024).

This model provides a framework for understanding the changes in $A_n$ that occur as a C₃ plant is exposed to successively higher concentrations of CO₂. Overall, the photosynthetic response to CO₂ under high light conditions can be divided into three separate ranges:

At low levels of CO₂ in the chloroplast, CO₂ assimilation is primarily limited by Rubisco activity; the maximum rate of Rubisco activity is denoted by $V_{cmax}$ .
At intermediate levels of CO₂ in the chloroplast, CO₂ assimilation is primarily limited by RuBP regeneration; the rate of RuBP regeneration is denoted by $J$ .
At high levels of CO₂ in the chloroplast, CO₂ assimilation is primarily limited by triose phosphate utilization (TPU); the maximum rate of TPU is denoted by $T_p$ .

More specifically, the model provides equations for potential RuBP carboxylation rates (as catalyzed by Rubisco) that are each limited by one of three important processes:

The Rubisco-limited carboxylation rate ( $W_c$ ).
The RuBP-regeneration-limited carboxylation rate ( $W_j$ ).
The triose-phosphate-utilization-limited carboxylation rate ( $W_p$ ).

Each of these rates depend on the CO₂ concentration in the chloroplast and other factors such as the incident light intensity. The actual RuBP carboxylation rate ( $V_c$ ) for a particular set of conditions is taken to be the smallest of the three potential rates. Then, the net CO₂ assimilation rate $A_n$ can be calculated from $V_c$ by including carbon losses due to photorespiration and mitochondrial respiration; the rate of mitochondrial respiration in the light is denoted by $R_L$ . It is also possible to calculate the potential net assimilation rates corresponding to each potential carboxylation rate: $A_c$ , $A_j$ , and $A_p$ . The plot below illustrates the three different assimilation ranges observed in a typical high-light A-C_i curve, as predicted by the FvCB model.

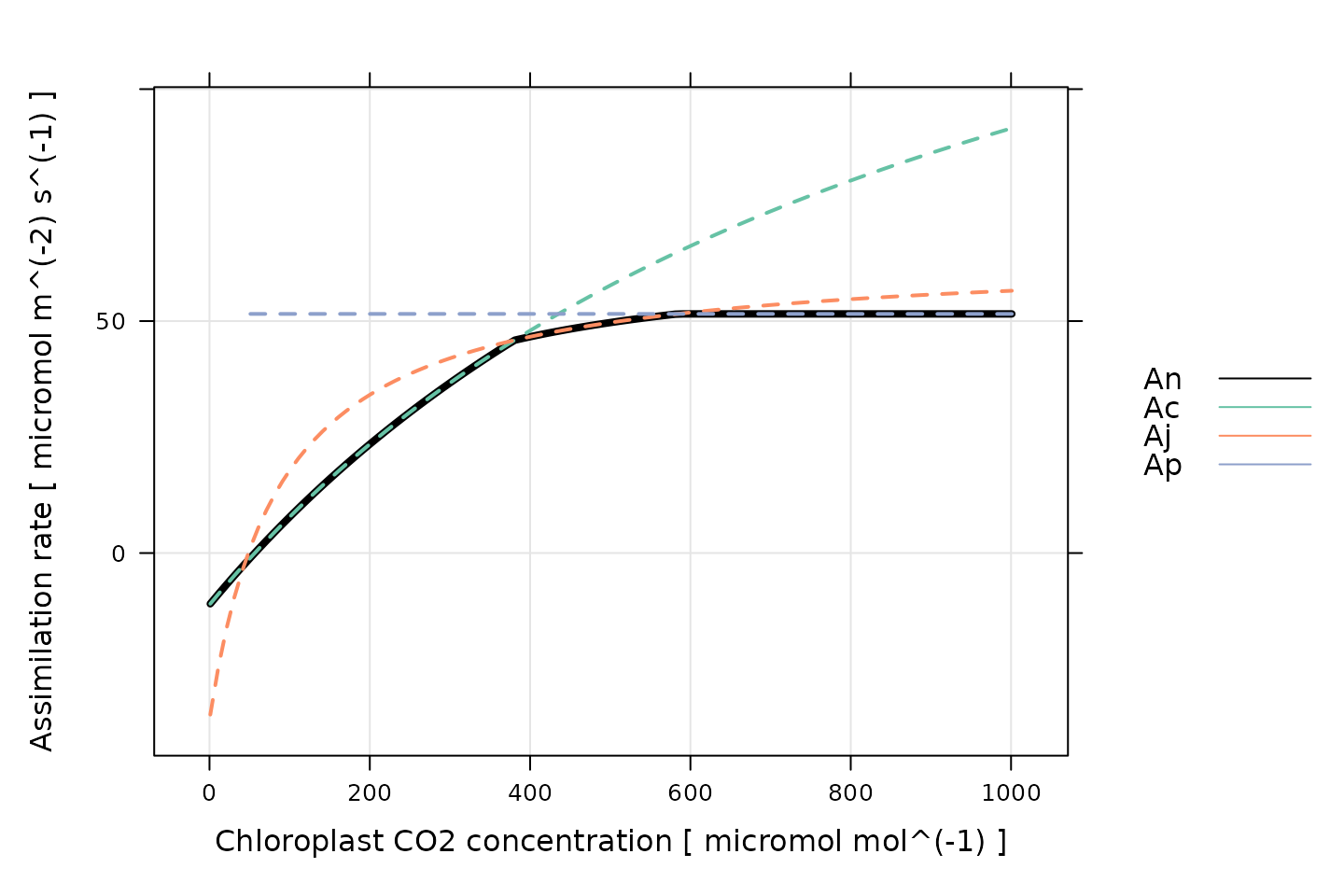
(Note: This figure was generated using the calculate_c3_assimilation function from the PhotoGEA package, and it represents the photosynethetic response of a C₃ leaf according to the FvCB model with Tp = 18 micromol m^(-2) s^(-1), J = 200 micromol m^(-2) s^(-1), RL = 1.8 micromol m^(-2) s^(-1), Vcmax = 125 micromol m^(-2) s^(-1), and a leaf temperature of 30 degrees C. Arrhenius temperature response parameters were taken from Sharkey et al. (2007).)

Thus, one of the most common reasons to measure an A-C_i curve is to interpret it in the context of this model. In other words, by fitting the model’s equations to a measured curve, it is possible to estimate values for $T_p$ , $J$ , $R_L$ , and $V_{cmax}$ . See the documentation for calculate_c3_assimilation for more information about these important quantities.

Practicalities

There are a few important practicalities to keep in mind when thinking about CO₂ response curves.

One point is that photosynthesis models generally predict the response of assimilation to the CO₂ concentration in the chloroplast ( $C_c$ ), but gas exchange measurements can only determine the CO₂ concentration in the leaf’s intercellular spaces ( $C_i$ ). Thus, an extra step is required when interpreting A-C_i curves. If the mesophyll conductance to CO₂ diffusion ( $g_{mc}$ ) is known, then it is possible to calculate values of $C_c$ from $A_n$ , $C_i$ , and $g_{mc}$ . Otherwise, it is typical to assume an infinite mesophyll conductance; in this case, $C_c = C_i$ , and the estimated values of $V_{cmax}$ and other parameters can be considered to be “effective values” describing the plant’s response to intercellular CO₂ rather than the true enzyme response to chloroplastic CO₂.

Another important point is that plants generally do not appreciate being starved of CO₂, so it is not usually possible to start a response curve at low CO₂ and proceed upwards. A more typical approach is to:

Begin at ambient atmospheric CO₂ levels.
Decrease towards a low value.
Return to ambient levels and wait for the plant to reacclimate; this waiting period is usually accomplished by logging several points at ambient CO₂ levels.
Increase to higher values.

When taking this approach, it therefore becomes necessary to remove the extra points measured at ambient CO₂ levels and to reorder the points according to their CO₂ values before plotting or analyzing them.

The Data

A-C_i curves are commonly measured using a portable photosynthesis system such as the Licor Li-6800. These machines record values of $A_n$ , $g_{sw}$ , $C_i$ , and many other important quantities. They produce two types of output files: plain-text and Microsoft Excel. It is often more convenient to work with the Excel files since the entries can be easily modified (for example, to remove an extraneous row or add a new column). On the other hand, it can be more difficult to access the file contents using other pieces of software such as R. However, the PhotoGEA package reduces this barrier by including tools for reading Licor Excel files in R, which will be demonstrated in the following section.

Loading Packages

As always, the first step is to load the packages we will be using. In addition to PhotoGEA, we will also use the lattice package for generating plots.

# Load required packages
library(PhotoGEA)
library(lattice)

If the lattice package is not installed on your R setup, you can install it by typing install.packages('lattice').

Loading Licor Data

The PhotoGEA package includes two files representing A-C_i curves measured using two Li-6800 instruments. The data is stored in Microsoft Excel files, and includes curves measured from two different crop species (tobacco and soybean) and several different plots of each. Each curve is a sixteen-point CO₂ response curve; in other words, the CO₂ concentration in the air surrounding the leaf was varied, and $A_n$ (among other variables) was measured at each CO₂ setpoint. Although these two files are based on real data, noise was added to it since it is unpublished, so these files should only be used as examples.

The files will be stored on your computer somewhere in your R package installation directory, and full paths to these files can be obtained with PhotoGEA_example_file_path:

# Define a vector of paths to the files we wish to load; in this case, we are
# loading example files included with the PhotoGEA package
file_paths <- c(
  PhotoGEA_example_file_path('c3_aci_1.xlsx'),
  PhotoGEA_example_file_path('c3_aci_2.xlsx')
)

(Note: When loading your own files for analysis, it is not advisable to use PhotoGEA_example_file_path as we have done here. Instead, file paths can be directly written, or files can be chosen using an interactive window. See Input Files below for more information.)

To actually read the data in the files and store them in R objects, we will use the read_gasex_file function from PhotoGEA. Since there are multiple files to read, we will call this function once for each file using lapply:

# Load each file, storing the result in a list
licor_exdf_list <- lapply(file_paths, function(fpath) {
  read_gasex_file(fpath, 'time')
})

The result from this command is an R list of “extended data frames” (abbreviated as exdf objects). The exdf class is a special data structure defined by the PhotoGEA package. In many ways, an exdf object is equivalent to a data frame, with the major difference being that an exdf object includes the units of each column. For more information, type ?exdf in the R terminal to access the built-in help menu entry, or check out the Working With Extended Data Frames vignette.

Generally, it is more convenient to work with a single exdf object rather than a list of them, so our next step will be to combine the objects in the list. This action can be accomplished using the rbind function, which combines table-like objects by their rows; in other words, it stacks two or more tables vertically. This action only makes sense if the tables have the same columns, so before we combine the exdf objects, we should make sure this is the case.

The PhotoGEA package includes a function called identify_common_columns that can be used to get the names of all columns that are present in all of the Licor files. Then, we can extract just those columns, and then combine the exdf objects into a single one.

# Get the names of all columns that are present in all of the Licor files
columns_to_keep <- do.call(identify_common_columns, licor_exdf_list)

# Extract just these columns
licor_exdf_list <- lapply(licor_exdf_list, function(x) {
  x[ , columns_to_keep, TRUE]
})

# Use `rbind` to combine all the data
licor_data <- do.call(rbind, licor_exdf_list)

Now we have a single R object called licor_data that includes all the data from several Licor Excel files. For more information about consolidating information from multiple files, see the Common Patterns section of the Working With Extended Data Frames vignette.

Validating the Data

Before attempting to fit the curves, it is a good idea to do some basic checks of the data to ensure it is organized properly and that it was measured properly.

Basic Checks

First, we should make sure there is a column in the data whose value uniquely identifies each curve. In this particular data set, several “user constants” were defined while making the measurements that help to identify each curve: instrument, species, and plot. However, neither of these columns alone are sufficient to uniquely identify each curve. We can solve this issue by creating a new column that combines the values from each of these:

# Create a new identifier column formatted like `instrument - species - plot`
licor_data[ , 'curve_identifier'] <-
  paste(licor_data[ , 'instrument'], '-', licor_data[ , 'species'], '-', licor_data[ , 'plot'])

The next step is to make sure that this column correctly identifies each response curve. To do this, we can use the check_response_curve_data function from PhotoGEA. Here we will supply the name of a column that should uniquely identify each response curve (curve_identifier), the expected number of points in each curve (16), the name of a “driving” column that should follow the same sequence in each curve (CO2_r_sp). If the data passes the checks, this function will have no output and will not produce any messages. (For more information, see the built-in help menu entry by typing ?check_response_curve_data.)

# Make sure the data meets basic requirements
check_response_curve_data(licor_data, 'curve_identifier', 16, 'CO2_r_sp')

However, if check_response_curve_data detects an issue, it will print a helpful message to the R terminal. For example, if we had specified the wrong number of points or the wrong identifier column, we would get error messages:

check_response_curve_data(licor_data, 'curve_identifier', 15)
#>       curve_identifier npts
#> 1 ripe1 - soybean - 5a   16
#> 2  ripe1 - tobacco - 1   16
#> 3  ripe1 - tobacco - 2   16
#> 4  ripe2 - soybean - 1   16
#> 5 ripe2 - soybean - 5b   16
#> 6  ripe2 - tobacco - 4   16
#> Error in check_response_curve_data(licor_data, "curve_identifier", 15): One or more curves does not have the expected number of points.

check_response_curve_data(licor_data, 'species', 16)
#>   species npts
#> 1 soybean   48
#> 2 tobacco   48
#> Error in check_response_curve_data(licor_data, "species", 16): One or more curves does not have the expected number of points.

check_response_curve_data(licor_data, 'curve_identifier', 16, 'Ci')
#>  [1] "Point 1 from curve `ripe1 - tobacco - 1` has value `Ci = 251.525996944688`, but the average value for this point across all curves is `Ci = 237.742020686325`"  
#>  [2] "Point 1 from curve `ripe1 - tobacco - 2` has value `Ci = 261.420818849899`, but the average value for this point across all curves is `Ci = 237.742020686325`"  
#>  [3] "Point 1 from curve `ripe2 - tobacco - 4` has value `Ci = 268.023119478639`, but the average value for this point across all curves is `Ci = 237.742020686325`"  
#>  [4] "Point 2 from curve `ripe1 - soybean - 5a` has value `Ci = 189.778318756111`, but the average value for this point across all curves is `Ci = 187.890931847939`" 
#>  [5] "Point 2 from curve `ripe1 - tobacco - 2` has value `Ci = 190.364626604515`, but the average value for this point across all curves is `Ci = 187.890931847939`"  
#>  [6] "Point 2 from curve `ripe2 - soybean - 1` has value `Ci = 195.64990814843`, but the average value for this point across all curves is `Ci = 187.890931847939`"   
#>  [7] "Point 2 from curve `ripe2 - tobacco - 4` has value `Ci = 189.683389404078`, but the average value for this point across all curves is `Ci = 187.890931847939`"  
#>  [8] "Point 3 from curve `ripe1 - tobacco - 2` has value `Ci = 140.739846550331`, but the average value for this point across all curves is `Ci = 138.989000725059`"  
#>  [9] "Point 3 from curve `ripe2 - soybean - 1` has value `Ci = 142.312320467618`, but the average value for this point across all curves is `Ci = 138.989000725059`"  
#> [10] "Point 3 from curve `ripe2 - soybean - 5b` has value `Ci = 143.562222433932`, but the average value for this point across all curves is `Ci = 138.989000725059`" 
#> [11] "Point 3 from curve `ripe2 - tobacco - 4` has value `Ci = 146.070064069876`, but the average value for this point across all curves is `Ci = 138.989000725059`"  
#> [12] "Point 4 from curve `ripe2 - soybean - 5b` has value `Ci = 113.289686896819`, but the average value for this point across all curves is `Ci = 107.426766159492`" 
#> [13] "Point 4 from curve `ripe2 - tobacco - 4` has value `Ci = 109.855903103213`, but the average value for this point across all curves is `Ci = 107.426766159492`"  
#> [14] "Point 5 from curve `ripe2 - tobacco - 4` has value `Ci = 85.5777210143503`, but the average value for this point across all curves is `Ci = 81.9169717791416`"  
#> [15] "Point 6 from curve `ripe2 - tobacco - 4` has value `Ci = 69.6297854655665`, but the average value for this point across all curves is `Ci = 68.5175017770492`"  
#> [16] "Point 7 from curve `ripe2 - tobacco - 4` has value `Ci = 56.8863754899374`, but the average value for this point across all curves is `Ci = 54.4173221075231`"  
#> [17] "Point 8 from curve `ripe1 - tobacco - 1` has value `Ci = 38.2025072855919`, but the average value for this point across all curves is `Ci = 36.0525184649295`"  
#> [18] "Point 8 from curve `ripe1 - tobacco - 2` has value `Ci = 37.1263965357958`, but the average value for this point across all curves is `Ci = 36.0525184649295`"  
#> [19] "Point 9 from curve `ripe2 - soybean - 1` has value `Ci = 283.443935342356`, but the average value for this point across all curves is `Ci = 277.293550282807`"  
#> [20] "Point 9 from curve `ripe2 - tobacco - 4` has value `Ci = 293.651577805789`, but the average value for this point across all curves is `Ci = 277.293550282807`"  
#> [21] "Point 10 from curve `ripe1 - tobacco - 2` has value `Ci = 265.953774610768`, but the average value for this point across all curves is `Ci = 260.791607349089`" 
#> [22] "Point 10 from curve `ripe2 - soybean - 5b` has value `Ci = 278.939936070802`, but the average value for this point across all curves is `Ci = 260.791607349089`"
#> [23] "Point 11 from curve `ripe1 - soybean - 5a` has value `Ci = 406.253997571488`, but the average value for this point across all curves is `Ci = 395.465043677258`"
#> [24] "Point 11 from curve `ripe2 - soybean - 5b` has value `Ci = 408.560591466166`, but the average value for this point across all curves is `Ci = 395.465043677258`"
#> [25] "Point 11 from curve `ripe2 - tobacco - 4` has value `Ci = 420.067730833784`, but the average value for this point across all curves is `Ci = 395.465043677258`" 
#> [26] "Point 12 from curve `ripe1 - tobacco - 1` has value `Ci = 547.105363904173`, but the average value for this point across all curves is `Ci = 508.989047311619`" 
#> [27] "Point 12 from curve `ripe1 - tobacco - 2` has value `Ci = 544.825019266542`, but the average value for this point across all curves is `Ci = 508.989047311619`" 
#> [28] "Point 12 from curve `ripe2 - soybean - 5b` has value `Ci = 540.706050036121`, but the average value for this point across all curves is `Ci = 508.989047311619`"
#> [29] "Point 12 from curve `ripe2 - tobacco - 4` has value `Ci = 557.813796419447`, but the average value for this point across all curves is `Ci = 508.989047311619`" 
#> [30] "Point 13 from curve `ripe1 - tobacco - 1` has value `Ci = 695.552175120025`, but the average value for this point across all curves is `Ci = 640.742220104825`" 
#> [31] "Point 13 from curve `ripe1 - tobacco - 2` has value `Ci = 714.400660938829`, but the average value for this point across all curves is `Ci = 640.742220104825`" 
#> [32] "Point 13 from curve `ripe2 - soybean - 5b` has value `Ci = 648.296844649221`, but the average value for this point across all curves is `Ci = 640.742220104825`"
#> [33] "Point 13 from curve `ripe2 - tobacco - 4` has value `Ci = 754.539509157309`, but the average value for this point across all curves is `Ci = 640.742220104825`" 
#> [34] "Point 14 from curve `ripe1 - tobacco - 1` has value `Ci = 873.847290736827`, but the average value for this point across all curves is `Ci = 764.016093410732`" 
#> [35] "Point 14 from curve `ripe1 - tobacco - 2` has value `Ci = 886.833187517944`, but the average value for this point across all curves is `Ci = 764.016093410732`" 
#> [36] "Point 14 from curve `ripe2 - tobacco - 4` has value `Ci = 955.187469706573`, but the average value for this point across all curves is `Ci = 764.016093410732`" 
#> [37] "Point 15 from curve `ripe1 - tobacco - 1` has value `Ci = 1174.23795813254`, but the average value for this point across all curves is `Ci = 994.214575601785`" 
#> [38] "Point 15 from curve `ripe1 - tobacco - 2` has value `Ci = 1162.50199383597`, but the average value for this point across all curves is `Ci = 994.214575601785`" 
#> [39] "Point 15 from curve `ripe2 - tobacco - 4` has value `Ci = 1234.06839380054`, but the average value for this point across all curves is `Ci = 994.214575601785`" 
#> [40] "Point 16 from curve `ripe1 - soybean - 5a` has value `Ci = 1376.24212413574`, but the average value for this point across all curves is `Ci = 1374.12936701593`"
#> [41] "Point 16 from curve `ripe1 - tobacco - 1` has value `Ci = 1489.79307180783`, but the average value for this point across all curves is `Ci = 1374.12936701593`" 
#> [42] "Point 16 from curve `ripe1 - tobacco - 2` has value `Ci = 1469.9939278736`, but the average value for this point across all curves is `Ci = 1374.12936701593`"  
#> [43] "Point 16 from curve `ripe2 - tobacco - 4` has value `Ci = 1509.57270639848`, but the average value for this point across all curves is `Ci = 1374.12936701593`"
#> Error in check_response_curve_data(licor_data, "curve_identifier", 16, : The curves do not all follow the same sequence of the driving variable.

Plotting the A-C_i Curves

One qualitative way to check the data is to simply create a plot of the A-C_i curves. In this situation, the lattice library makes it simple to include each curve as its own separate subplot of a figure. For example:

# Plot all A-Ci curves in the data set
xyplot(
  A ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']'),
  ylab = paste('Net CO2 assimilation rate [', licor_data$units$A, ']')
)

Whoops! Why do these curves look so strange? Well, some of the issues are related to the sequence of CO₂ values that was used when measuring the curves. As discussed in Practicalities, there are several repeated points logged at the same CO₂ concentration, and the points are not logged in order of ascending or descending concentration. In fact, the sequence of CO₂ setpoints is as follows:

licor_data[licor_data[, 'curve_identifier'] == 'ripe2 - soybean - 1', 'CO2_r_sp']
#>  [1]  400  300  200  150  100   75   50   20  400  400  600  800 1000 1200 1500
#> [16] 1800

Ideally, we would like to remove the ninth and tenth points (where the setpoint has been reset to 400 to allow the leaf to reacclimate to ambient CO₂ levels), and reorder the data so it is arranged from low to high values of Ci. This can be done using the organize_response_curve function from PhotoGEA:

# Remove points with duplicated `CO2_r_sp` values and order by `Ci`
licor_data <- organize_response_curve_data(
    licor_data,
    'curve_identifier',
    c(9, 10),
    'Ci'
)

Now we can plot them again:

# Plot all A-Ci curves in the data set
xyplot(
  A ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']'),
  ylab = paste('Net CO2 assimilation rate [', licor_data$units$A, ']')
)

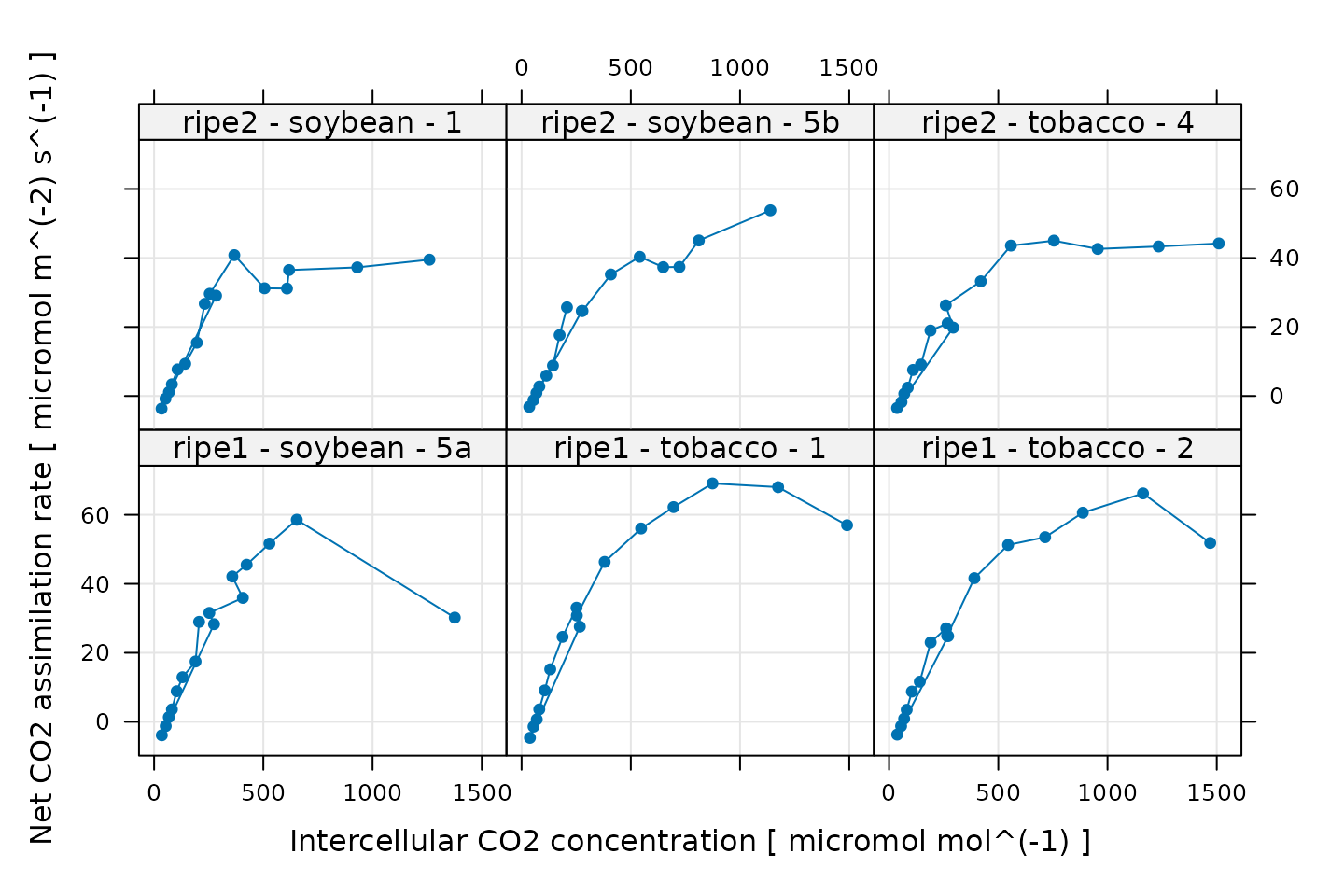
They still look a bit strange, but this is related to the noise that was intentionally added to the data. Three curves exhibit a sharp and likely unrealistic downturn in assimilation at their highest values of $C_i$ . These will pose a problem for fitting, and we will remove them later after making some other quality checks.

Additional Plots for Qualitative Validation

Sometimes a Licor will override the temperature or humidity controls while making measurements; in this case, conditions inside the measurement chamber may not be stable, and we may wish to exclude some of these points. We can check for these types of issues by making more plots. In the following sections, we will generate several different plots to check each curve for quality.

Humidity Control

# Make a plot to check humidity control
xyplot(
  RHcham + `Humidifier_%` + `Desiccant_%` ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  ylim = c(0, 100),
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']')
)

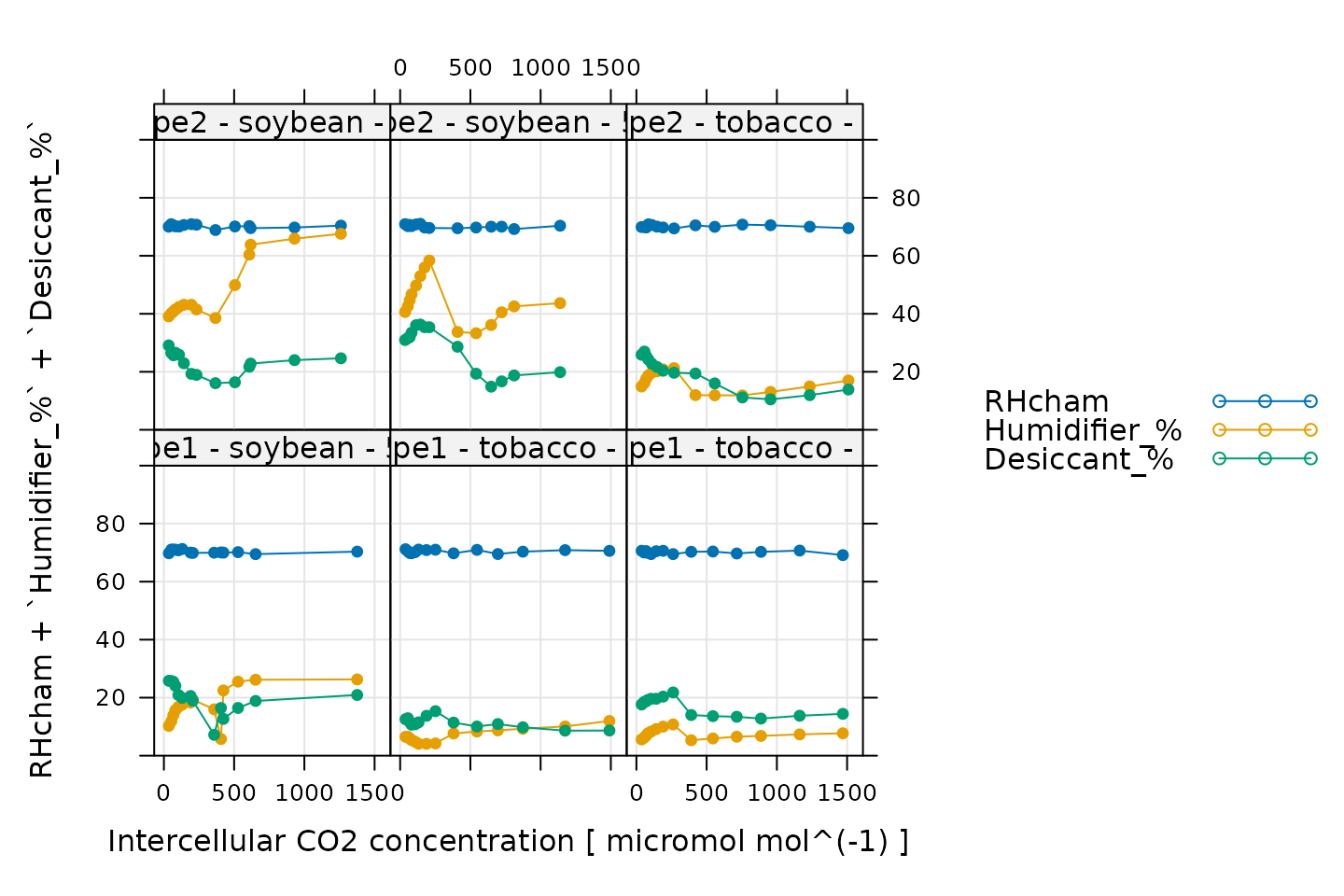
Here, Humidifier_% and Desiccant_% represent the flow from the humidifier and desiccant columns, where a value of 0 indicates that the valve to the column is fully closed and a value of 100 indicates that the valve to the column is fully opened. RHcham represents the relative humidity inside the chamber as a percentage (in other words, as a value between 0 and 100).

When these curves were measured, a chamber humidity setpoint was specified. So, when looking at this plot, we should check that the relative humidity is fairly constant during each curve. Typically, this should be accompanied by relatively smooth changes in the valve percentages as they accomodate changes in ambient humidity and leaf photosynthesis. In this plot, all the data looks good.

Temperature Control

# Make a plot to check temperature control
xyplot(
  TleafCnd + Txchg ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  ylim = c(25, 40),
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']'),
  ylab = paste0('Temperature (', licor_data$units$TleafCnd, ')')
)

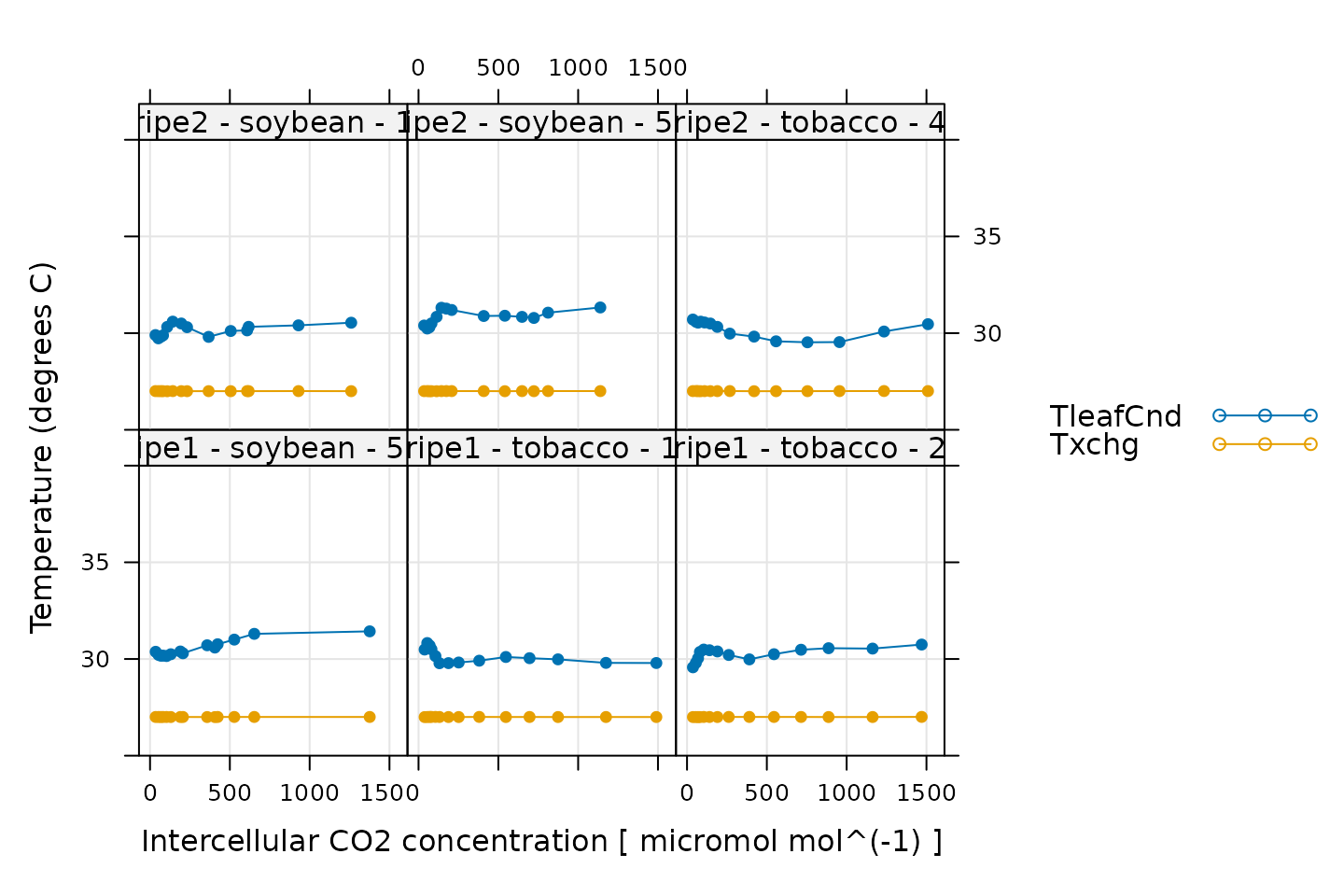
Here, TleafCnd is the leaf temperature measured using a thermocouple, and Txchg is the temperature of the heat exhanger that is used to control the air temperature in the measurement instrument. When these curves were measured, an exchanger setpoint was specified. So, when looking at this plot, we should check that Txchg is constant during each curve and that the leaf temperature does not vary in an erratic way. In this plot, all the data looks good.

CO₂ Control

# Make a plot to check CO2 control
xyplot(
  CO2_s + CO2_r + CO2_r_sp ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']'),
  ylab = paste0('CO2 concentration (', licor_data$units$CO2_r, ')')
)

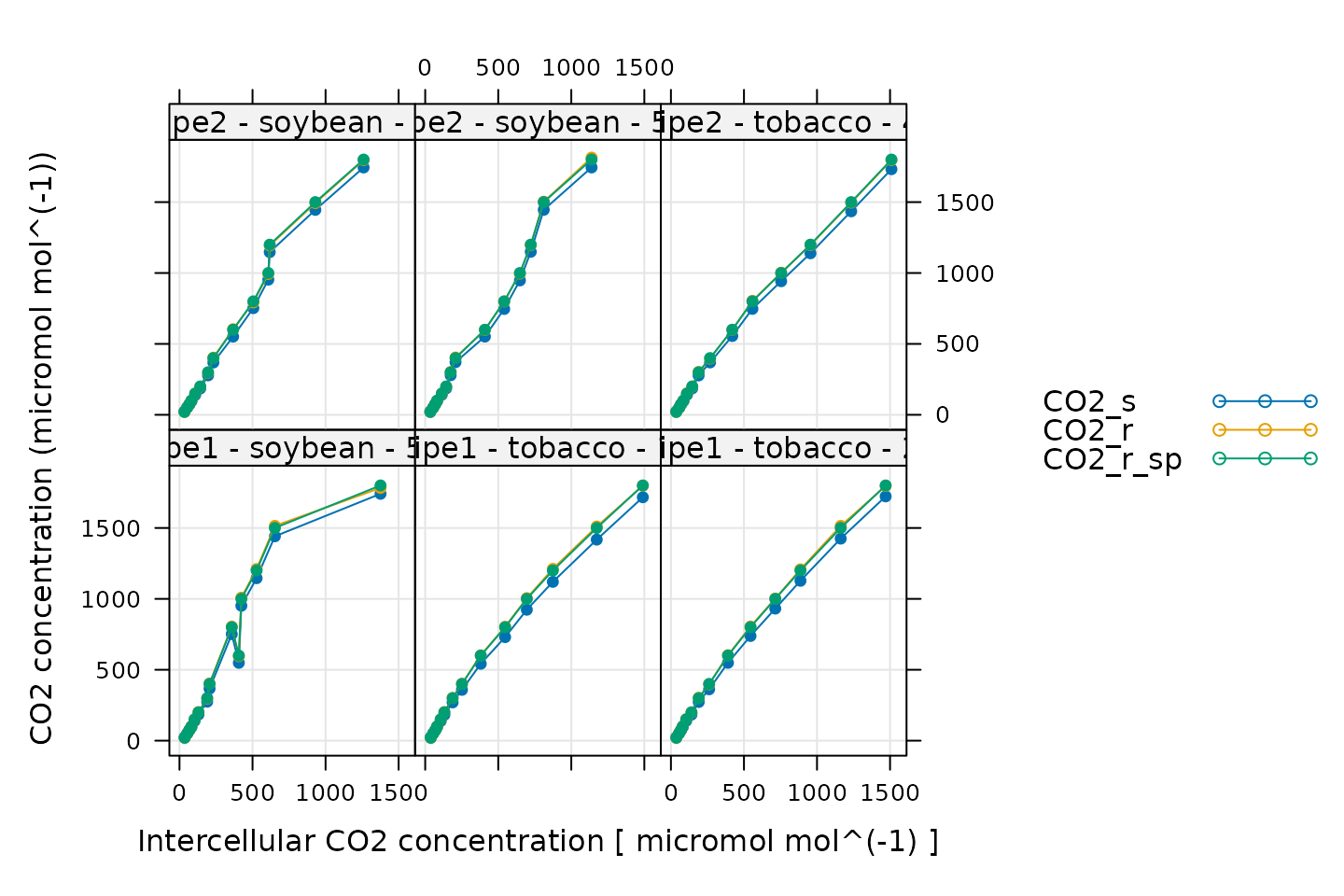
Here, CO2_s is the CO₂ concentration in the sample cell, CO2_r is the CO₂ concentration in the reference cell, and CO2_r_sp is the setpoint for CO2_r. When these curves were measured, a sequence of CO2_r values was specified, so, when looking at this plot, we should check that CO2_r is close to CO2_r_sp. We also expect that CO2_s should be a bit lower than CO2_r because the leaf in the sample chamber is assimilating CO₂, which should reduce its concentration in the surrounding air. (An exception to this rule occurs at very low values of CO2_r_sp, since in this case there is not enough carbon available to assimilate, and the leaf actually releases CO₂ due to respiration.) In this plot, all the data looks good.

Stability

# Make a plot to check stability criteria
xyplot(
  `A:OK` + `gsw:OK` + Stable ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']')
)

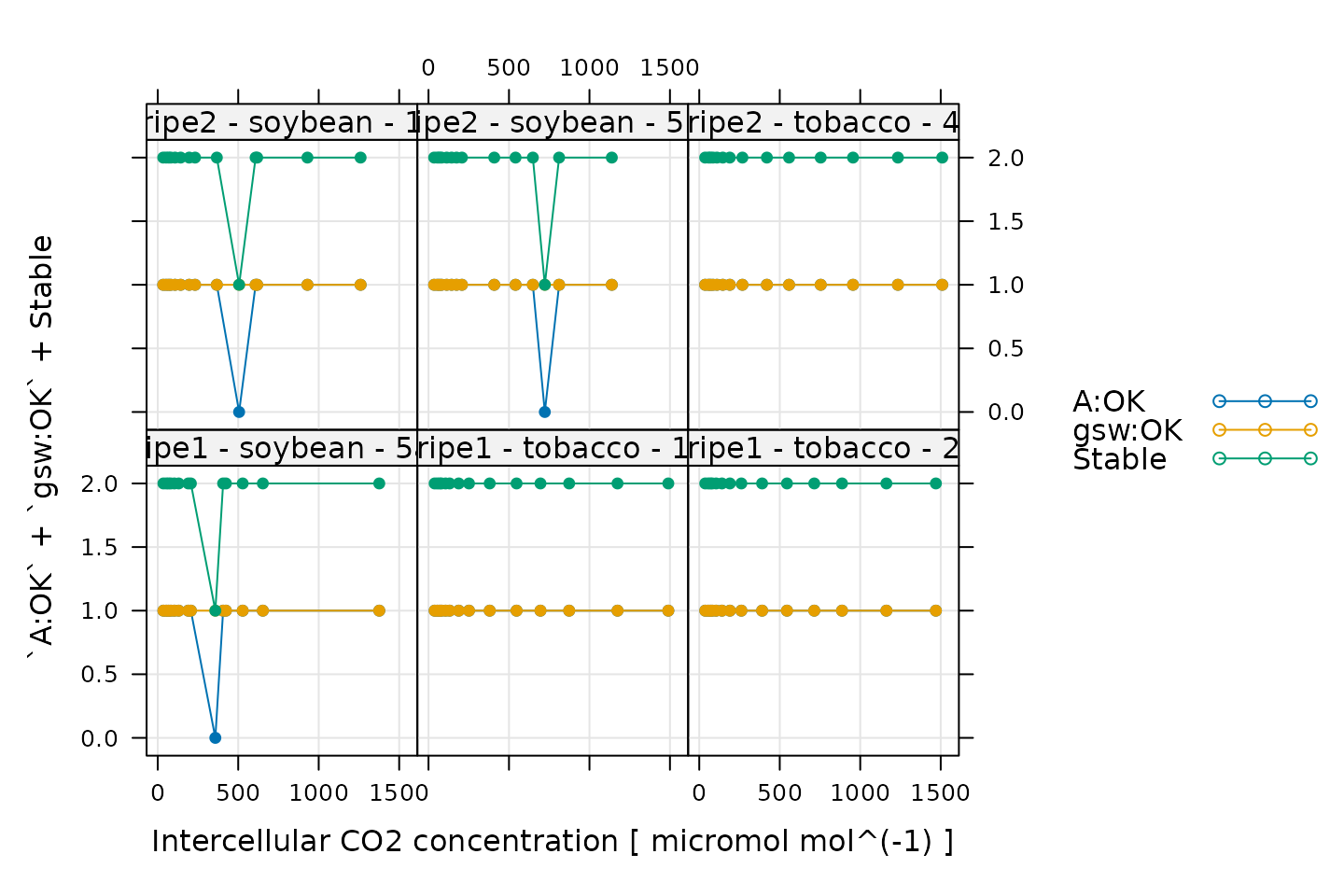
When measuring response curves with a Licor, it is possible to specify stability criteria for each point in addition to minimum and maximum wait times. In other words, once the set point for the driving variable is changed, the machine waits until the stability criteria are met; there is a minimum waiting period, and also a maximum to prevent the machine from waiting for too long.

When these curves were measured, stability criteria were supplied for the net assimilation rate A and the stomatal conductance gsw. The stability status for each was stored in the log file because the appropriate logging option for stability was set. Now, for each point, it is possible to check whether stability was achieved or whether the point was logged because the maximum waiting period had been met. If the maximum waiting period is reached and the plant has still not stabilized, the data point may be unreliable, so it can be helpful to check this information.

In the plot, A:OK indicates whether A was stable (0 for no, 1 for yes), gsw:OK indicates whether gsw was stable (0 for no, 1 for yes), and Stable indicates the total number of stability conditions that were met. So, we are looking for points where Stable is 2. Otherwise, we can check the other traces to see whether A or gsw was unstable.

Comparing these plots with the ones in Plotting the A-C_i Curves, it seems that the unstable points correspond with some of the “odd-looking” points in the A-C_i curves, so it is probably a good idea to remove them before fitting the data.

Cleaning the Licor Data

While checking over the plots in the previous sections, two issues were noticed: (1) some points were logged before stability was achieved and (2) some curves have strange points at high $C_i$ . In this section, we will demonstrate how to remove the unstable and unusual points.

The following command will keep only the points where Stable is exactly 2; this condition means that all of the stability criteria were satisfied. Sometimes, following this procedure, a curve will have very few stable points remaining; it is usually a good idea to automatically exclude any curve with fewer than three stable points.

# Only keep points where stability was achieved
licor_data <- licor_data[licor_data[, 'Stable'] == 2, , TRUE]

# Remove any curves that have fewer than three remaining points
npts <- by(licor_data, licor_data[, 'curve_identifier'], nrow)
ids_to_keep <- names(npts[npts > 2])
licor_data <- licor_data[licor_data[, 'curve_identifier'] %in% ids_to_keep, , TRUE]

Next, we can use the remove_points function from PhotoGEA to exclude the points where there is a decrease in $A$ at high $C_i$ . It just so happens that all of these points were measured by the ripe1 instrument and occur at the highest CO₂ setpoint value, so it is easy to specify them all at once:

# Remove points where `instrument` is `ripe1` and `CO2_r_sp` is 1800
licor_data <- remove_points(
  licor_data,
  list(instrument = 'ripe1', CO2_r_sp = 1800)
)

Fitting Licor Data

Now that we have checked the data quality, we are ready to perform the fitting. In order to fit the curves, there are several required pieces of information that are not included in the Licor data files as produced by the instrument: values of the total pressure, values of the chloroplast CO₂ concentration $C_c$ , and temperature-dependent values of important photosynthetic parameters such as $\Gamma^*$ . However, the PhotoGEA package includes three functions to help with these calculations: calculate_total_pressure, apply_gm, and calculate_arrhenius. Each of these requires an exdf object containing Licor data. The units for each required column will be checked in an attempt to avoid unit-related errors. More information about these functions can be obtained from the built-in help system by typing ?calculate_total_pressure, ?apply_gm, or ?calculate_arrhenius.

Another important consideration is that apply_gm requires values of the mesophyll conductance to CO₂. Values of mesophyll conductance can be specified using the set_variable function from PhotoGEA. Here we will set gmc = 1.0 mol / m^2 / s / bar for tobacco and gmc = Inf for soybean; in this case, the soybean parameters determined by the fitting process will be “effective” parameters. Then we will calculate values of $C_c$ , and use Arrhenius parameters from Sharkey et al. (2007) to calculate the temperature-dependent inputs:

# Calculate total pressure in the Licor chamber
licor_data <- calculate_total_pressure(licor_data)

# Specify separate mesophyll conductance values for each species
licor_data <- set_variable(
  licor_data, 'gmc', 'mol m^(-2) s^(-1) bar^(-1)',
  id_column = 'species',
  value_table = list(tobacco = 1.0, soybean = Inf)
)

# Calculate Cc
licor_data <- apply_gm(licor_data)

# Calculate temperature-dependent values of C3 photosynthetic parameters
licor_data <- calculate_arrhenius(licor_data, c3_arrhenius_sharkey)

Together, these functions add several new columns to licor_data, including gmc, Cc, Gamma_star, and others. With this information, we are now ready to perform the fitting procedure. For this operation, we can use the fit_c3_aci function from the PhotoGEA package, which fits a single response curve to extract the values of key photosynthetic parameters. To apply this function to each curve in a larger data set and then consolidate the results, we can use it in conjunction with by and consolidate, which are also part of PhotoGEA. (For more information about these functions, see the built-in help menu entries by typing ?fit_c3_aci, ?by.exdf, or ?consolidate, or check out the Common Patterns section of the Working With Extended Data Frames vignette.) Together, these functions will split apart the main data using the curve identifier column we defined before (Basic Checks), fit each A-C_i curve using the FvCB model discussed in Understanding C₃A-C_i Curves, and return the resulting parameters and fits:

# The default optimizer uses randomness, so we will set a seed to ensure the
# results from this fit are always identical
set.seed(1234)

# Fit the C3 A-Ci curves
c3_aci_results <- consolidate(by(
  licor_data,                       # The `exdf` object containing the curves
  licor_data[, 'curve_identifier'], # A factor used to split `licor_data` into chunks
  fit_c3_aci,                       # The function to apply to each chunk of `licor_data`
  Ca_atmospheric = 420              # Additional argument passed to `fit_c3_aci`
))

Note that in this command, we used the default fitting settings. In this case, we will vary all five key photosynthetic parameters: $R_L$ , $V_{cmax}$ , $J$ , $T_p$ , and $\alpha_{old}$ .

Viewing the Fitted Curves

Having made the fits, it is now a good idea to visually check them, making sure they look reasonable. This can be done using a built-in plotting function called plot_c3_aci_fit. In addition to the fitted values of An, the output also includes values of the potential limiting rates Ac, Aj, and Ap, as well as the estimated operating point.

# Plot the C3 A-Cc fits (including limiting rates)
plot_c3_aci_fit(c3_aci_results, 'curve_identifier', 'Ci', ylim = c(-10, 80))

In general, these fits look good. There are a few specific things to notice:

The fitted values of An closely match the measured ones. This is a good sign.
Each curve begins with a Rubisco-limited portion (where An = Ac). This is expected for light-saturated A-C_i curves.
Some curves do not have values of Aj. This means that no points were identified as being limited by RuBP regeneration. It is not possible to estimate values of J from such curves.
Some curves do not have values of Ap. This means that no points were identified as being limited by TPU. It is not possible to estimate values of Tp from such curves.
One curve is almost entirely limited by Rubisco activity. Based on its values of Ci, it seems that this plant’s stomata did not fully open during the measurement, almost fully restricting the measured assimilation values to the Rubisco-limited range. For this curve, the optimizer identified just one point as being RuBP-regeneration-limited, so the associated value of J may not be reliable.

It is typical that some parameters cannot be estimated from some A-C_i curves. This is an unavoidable consquence of the inherent variability between plant leaves.

Checking the residuals is also a powerful way to gauge the quality of a fit. The output from fit_c3_aci includes the residuals (calculated as A - A_fit) in its output, so it is easy to plot them:

# Plot the residuals
xyplot(
  A_residuals ~ Ci | curve_identifier,
  data = c3_aci_results$fits$main_data,
  type = 'b',
  pch = 16,
  grid = TRUE,
  xlab = paste0('Intercellular CO2 concentration (', c3_aci_results$fits$units$Ci, ')'),
  ylab = paste0('Assimilation rate residual (measured - fitted)\n(', c3_aci_results$fits$units$A, ')')
)

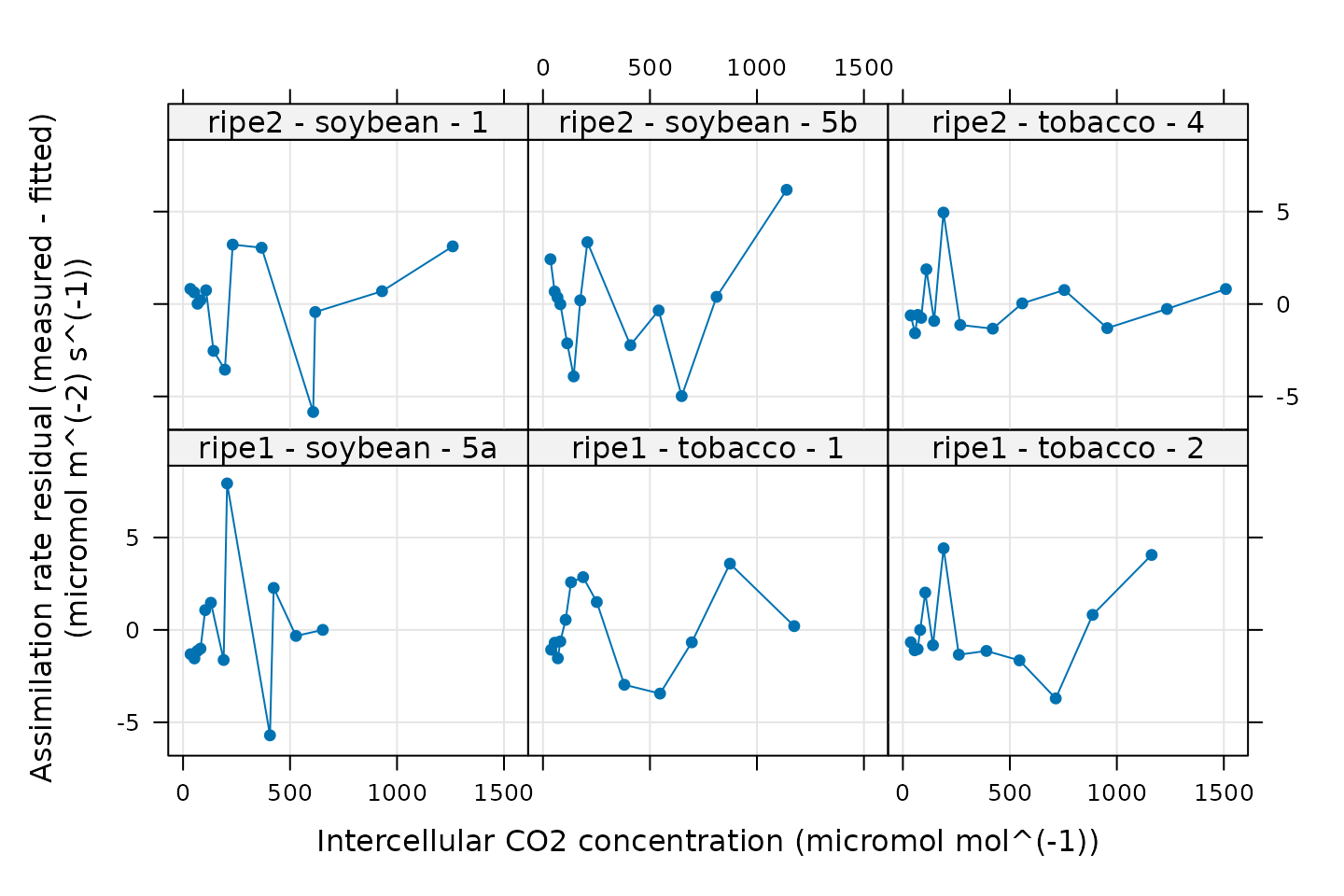
A good fit should produce small and randomly-distributed residuals; here there is no clear pattern to the residuals, so this model is able to reproduce the measured values well.

Examining the Results

Accessing Best-Fit Estimates and Confidence Intervals

Each fit returns best-fit values and confidence limits for each parameter, which are stored in c3_aci_results$parameters, another exdf object. For example, we can look at the estimated $J$ values from each curve as follows:

# View values of J from each fit
c3_aci_results$parameters[, c('curve_identifier', 'J_at_25_lower', 'J_at_25', 'J_at_25_upper')]
#>       curve_identifier J_at_25_lower  J_at_25 J_at_25_upper
#> 1 ripe1 - soybean - 5a      183.4704       NA           Inf
#> 2  ripe1 - tobacco - 1      233.0200 240.2729      247.5259
#> 3  ripe1 - tobacco - 2      204.0791 211.6087      219.1383
#> 4  ripe2 - soybean - 1      160.0126       NA           Inf
#> 5 ripe2 - soybean - 5b      152.3074 160.9141      169.5208
#> 6  ripe2 - tobacco - 4      166.3857       NA           Inf

Here we can see that some curves have an upper limit of infinity (Inf) and a best-fit value of “not available” (NA). Comparing this table to the figure showing the fits, we can see that these are the curves where one or fewer points are limited by RuBP regeneration. For these curves, values of J cannot be reliably estimated, so fit_c3_aci returns a value of NA for J_at_25.

In contrast, each curve has an associated value of $V_{cmax}$ with a finite confidence interval:

# View values of Vcmax from each fit
c3_aci_results$parameters[, c('curve_identifier', 'Vcmax_at_25_lower', 'Vcmax_at_25', 'Vcmax_at_25_upper')]
#>       curve_identifier Vcmax_at_25_lower Vcmax_at_25 Vcmax_at_25_upper
#> 1 ripe1 - soybean - 5a          96.90012   103.76130         111.42321
#> 2  ripe1 - tobacco - 1         143.54375   152.22336         166.48570
#> 3  ripe1 - tobacco - 2         117.99127   126.80601         135.62073
#> 4  ripe2 - soybean - 1         102.06632   108.82793         121.10386
#> 5 ripe2 - soybean - 5b         105.28716   122.01141         138.73517
#> 6  ripe2 - tobacco - 4          89.34372    93.87686          99.47903

Visualizing Average Best-Fit Parameters

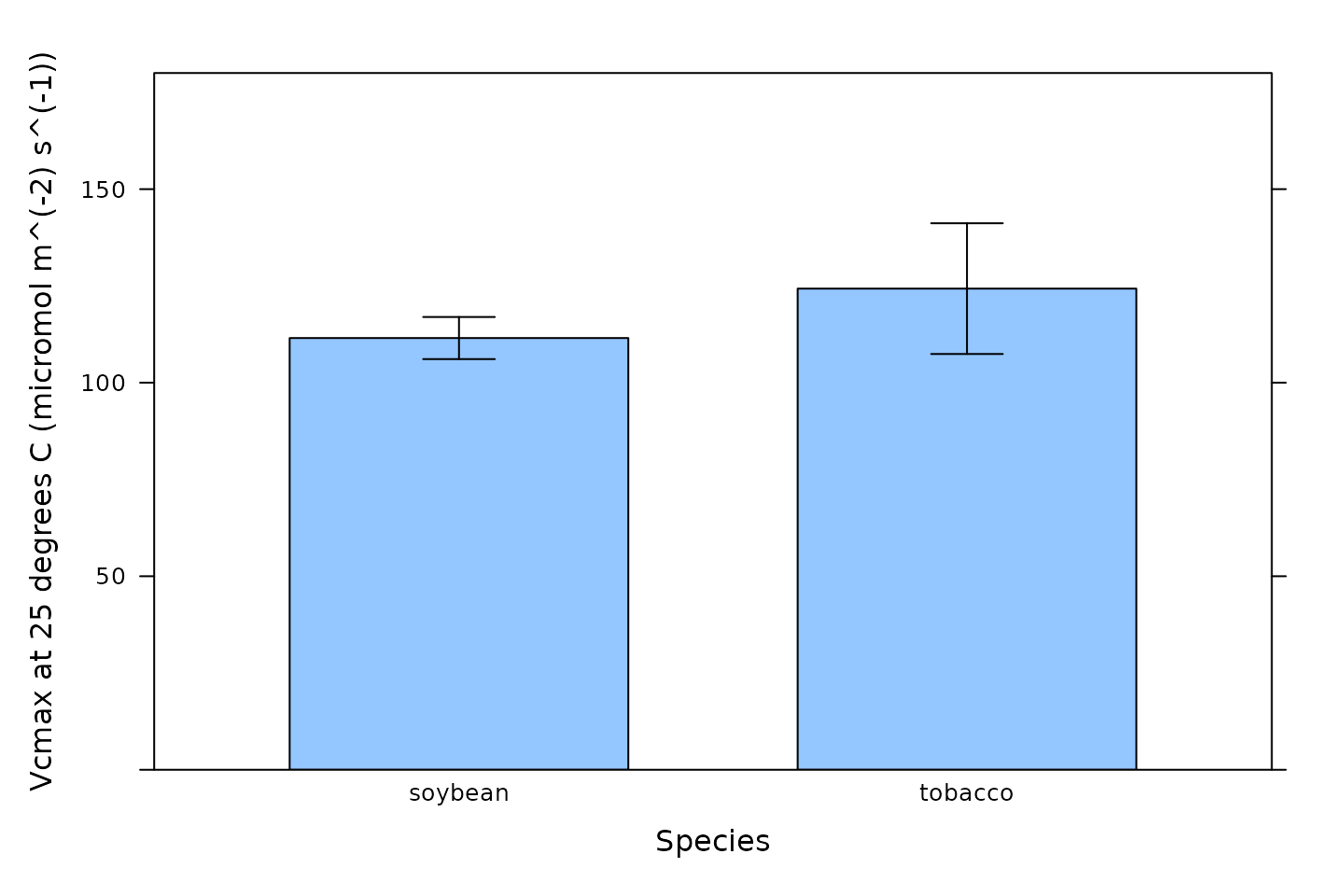
We can also visualize the best-fit parameters using plots. One way to do this is by using the barchart_with_errorbars function from PhotoGEA to create barcharts of the average values for each species. This function will ignore any NA values from curves where a parameter could not be reliably estimated, and the error bars will show the standard error of the mean for each species.

# Make a barchart showing average Vcmax values
barchart_with_errorbars(
  c3_aci_results$parameters[, 'Vcmax_at_25'],
  c3_aci_results$parameters[, 'species'],
  ylim = c(0, 180),
  xlab = 'Species',
  ylab = paste0('Vcmax at 25 degrees C (', c3_aci_results$parameters$units$Vcmax_at_25, ')')
)

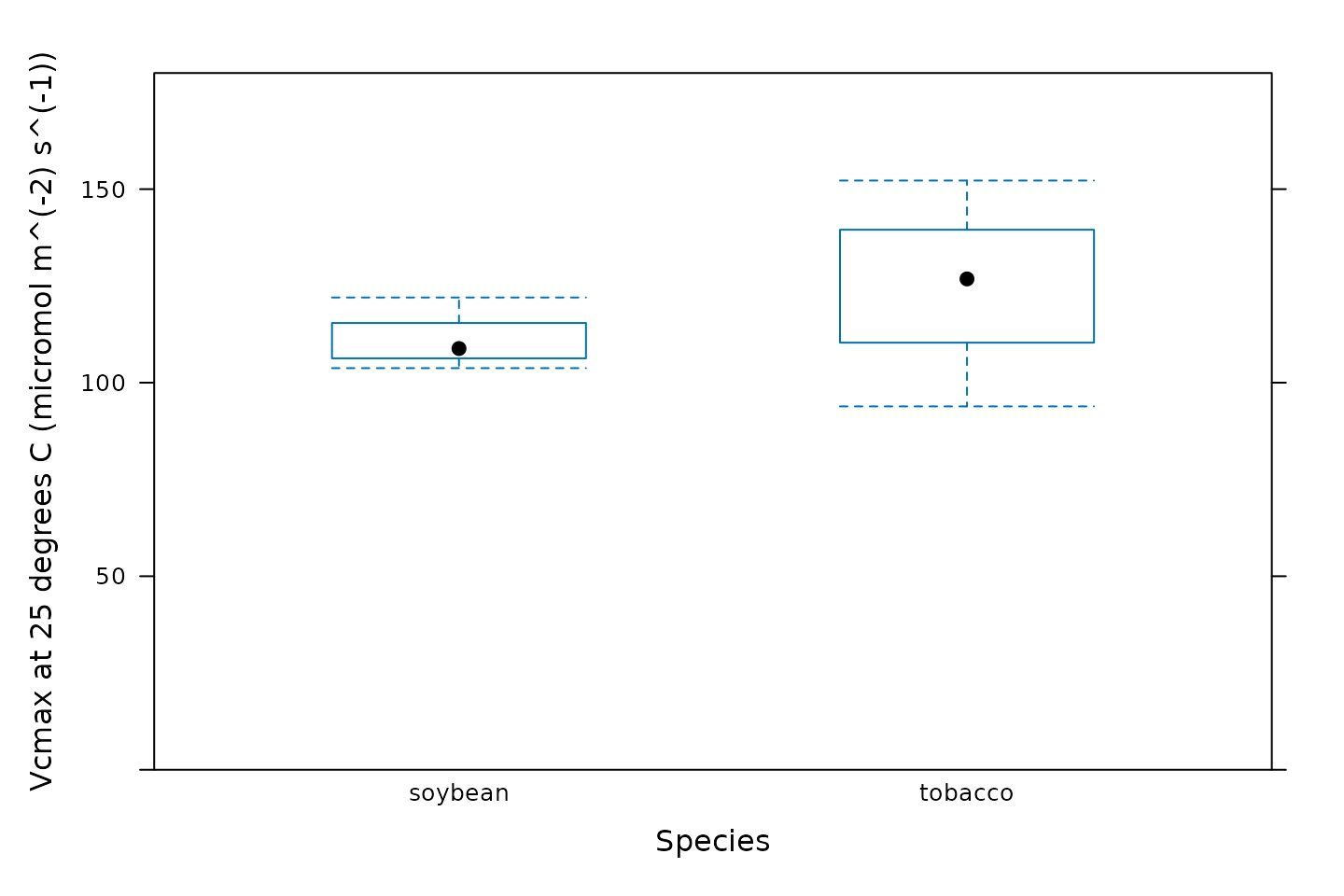
Another option is to create box-whisper plots using the bwplot function from the lattice package:

# Make a boxplot showing the distribution of Vcmax values
bwplot(
  Vcmax_at_25 ~ species,
  data = c3_aci_results$parameters$main_data,
  ylim = c(0, 180),
  xlab = 'Species',
  ylab = paste0('Vcmax at 25 degrees C (', c3_aci_results$parameters$units$Vcmax_at_25, ')')
)

Calculating Average Best-Fit Parameters

We can also calculate average values and standard errors of the best-fit parameters for each species using the basic_stats function from PhotoGEA:

# Compute the average and standard error of each parameter for each species
c3_aci_averages <- basic_stats(c3_aci_results$parameters, 'species')

# View the averages and errors
columns_to_view <- c(
  'species',
  'Vcmax_at_25_avg', 'Vcmax_at_25_stderr',
  'J_at_25_avg', 'J_at_25_stderr',
  'RL_at_25_avg', 'RL_at_25_stderr',
  'Tp_avg', 'Tp_stderr'
)

c3_aci_averages[ , columns_to_view]
#>   species Vcmax_at_25_avg Vcmax_at_25_stderr J_at_25_avg J_at_25_stderr
#> 1 soybean        111.5335           5.439266    160.9141             NA
#> 2 tobacco        124.3021          16.889650    225.9408       14.33209
#>   RL_at_25_avg RL_at_25_stderr   Tp_avg Tp_stderr
#> 1     1.934000       0.5719046 12.99084        NA
#> 2     1.964341       0.2165851 14.97514        NA

Other Ideas for Synthesizing Results

Statistical tests to check for differences between groups can be performed within R using other packages such as onewaytests or DescTools. Alternatively, the parameter values can be exported to a comma-separated-value (CSV) file and analyzed in another software environment like jmp.

Customizing Your Script

Note that most of the commands in this vignette have been written in a general way so they can be used as the basis for your own analysis script (see Commands From This Document). In order to use them in your own script, some or all of the following changes may be required. There may also be others not specifically mentioned here.

Input Files

The file paths specified in file_paths will need to be modified so they point to your Licor files. One way to do this in your own script is to simply write out relative or absolute paths to the files you wish to load. For example, you could replace the previous definition of file_paths with this one:

# Define a vector of paths to the files we wish to load
file_paths <- c(
  'myfile1.xlsx',        # `myfile1.xlsx` must be in the current working directory
  'C:/documents/myfile2' # This is an absolute path to `myfile2`
)

You may also want to consider using the choose_input_licor_files function from PhotoGEA; this function will create a pop-up browser window where you can interactively select a set of files. Sometimes this is more convenient than writing out file paths or names. For example, you could replace the previous definition of file_paths with this one:

# Interactively define a vector of paths to the files we wish to load
file_paths <- choose_input_licor_files()

Unfortunately, choose_input_licor_files is only available in interactive R sessions running on Microsoft Windows, but there is also a platform-independent option: choose_input_files. See the Translation section of the Developing a Data Analysis Pipeline vignette for more details.

Curve Identifier

Depending on which user constants are defined in your Licor Excel files, you may need to modify the definition of the curve_identifier column.

Data Cleaning

Depending on the qualitative data checks, you may need to change the input arguments to remove_points. It might also not be necessary to remove the unstable points before performing the fits. Often, it is helpful to not perform any data cleaning at first, and then remove problematic points if they seem to cause problems with the fits.

Plots

You may need to change the axis limits in some or all of the plots. Alternatively, you can remove them, allowing xyplot to automatically choose them for you.

You may also want to consider using the pdf_print function from PhotoGEA to save some or all of your plots as PDFs. See the help page for more info: ?pdf_print.

Saving Results

You may want to use write.csv.exdf to save some or all of the fitting results as CSV files. When writing the contents of an exdf object to a CSV file, using write.csv.exdf rather than write.csv will ensure that units are included with each column.

For example, the following commands will allow you to interactively choose output filenames for the resulting CSV files:

write.csv.exdf(c3_aci_results$fits, file.choose())
write.csv.exdf(c3_aci_results$parameters, file.choose())
write.csv.exdf(c3_aci_averages, file.choose())

Commands From This Document

The following code chunk includes all the central commands used throughout this document. They are compiled here to make them easy to copy/paste into a text file to initialize your own script. Annotation has also been added to clearly indicate the four steps involved in data analysis, as described in the Developing a Data Analysis Pipeline vignette.

###
### PRELIMINARIES:
### Loading packages, defining constants, creating helping functions, etc.
###

# Load required packages
library(PhotoGEA)
library(lattice)

###
### TRANSLATION:
### Creating convenient R objects from raw data files
###

## IMPORTANT: When loading your own files, it is not advised to use
## `PhotoGEA_example_file_path` as in the code below. Instead, write out the
## names or use the `choose_input_licor_files` function.

# Define a vector of paths to the files we wish to load; in this case, we are
# loading example files included with the PhotoGEA package
file_paths <- c(
  PhotoGEA_example_file_path('c3_aci_1.xlsx'),
  PhotoGEA_example_file_path('c3_aci_2.xlsx')
)

# Load each file, storing the result in a list
licor_exdf_list <- lapply(file_paths, function(fpath) {
  read_gasex_file(fpath, 'time')
})

# Get the names of all columns that are present in all of the Licor files
columns_to_keep <- do.call(identify_common_columns, licor_exdf_list)

# Extract just these columns
licor_exdf_list <- lapply(licor_exdf_list, function(x) {
  x[ , columns_to_keep, TRUE]
})

# Use `rbind` to combine all the data
licor_data <- do.call(rbind, licor_exdf_list)

###
### VALIDATION:
### Organizing the data, checking its consistency and quality, cleaning it
###

# Create a new identifier column formatted like `instrument - species - plot`
licor_data[ , 'curve_identifier'] <-
  paste(licor_data[ , 'instrument'], '-', licor_data[ , 'species'], '-', licor_data[ , 'plot'])

# Make sure the data meets basic requirements
check_response_curve_data(licor_data, 'curve_identifier', 16, 'CO2_r_sp')

# Remove points with duplicated `CO2_r_sp` values and order by `Ci`
licor_data <- organize_response_curve_data(
    licor_data,
    'curve_identifier',
    c(9, 10),
    'Ci'
)

# Plot all A-Ci curves in the data set
xyplot(
  A ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']'),
  ylab = paste('Net CO2 assimilation rate [', licor_data$units$A, ']')
)

# Make a plot to check humidity control
xyplot(
  RHcham + `Humidifier_%` + `Desiccant_%` ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  ylim = c(0, 100),
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']')
)

# Make a plot to check temperature control
xyplot(
  TleafCnd + Txchg ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  ylim = c(25, 40),
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']'),
  ylab = paste0('Temperature (', licor_data$units$TleafCnd, ')')
)

# Make a plot to check CO2 control
xyplot(
  CO2_s + CO2_r + CO2_r_sp ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']'),
  ylab = paste0('CO2 concentration (', licor_data$units$CO2_r, ')')
)

# Make a plot to check stability criteria
xyplot(
  `A:OK` + `gsw:OK` + Stable ~ Ci | curve_identifier,
  data = licor_data$main_data,
  type = 'b',
  pch = 16,
  auto = TRUE,
  grid = TRUE,
  xlab = paste('Intercellular CO2 concentration [', licor_data$units$Ci, ']')
)

## IMPORTANT: When analyzing your own files, it is not advised to remove any
## points for the initial fits. Only remove unstable or unusual points if it is
## necessary in order to get good fits.

# Only keep points where stability was achieved
licor_data <- licor_data[licor_data[, 'Stable'] == 2, , TRUE]

# Remove any curves that have fewer than three remaining points
npts <- by(licor_data, licor_data[, 'curve_identifier'], nrow)
ids_to_keep <- names(npts[npts > 2])
licor_data <- licor_data[licor_data[, 'curve_identifier'] %in% ids_to_keep, , TRUE]

# Remove points where `instrument` is `ripe1` and `CO2_r_sp` is 1800
licor_data <- remove_points(
  licor_data,
  list(instrument = 'ripe1', CO2_r_sp = 1800)
)

###
### PROCESSING:
### Extracting new pieces of information from the data
###

# Calculate total pressure in the Licor chamber
licor_data <- calculate_total_pressure(licor_data)

# Specify separate mesophyll conductance values for each species
licor_data <- set_variable(
  licor_data, 'gmc', 'mol m^(-2) s^(-1) bar^(-1)',
  id_column = 'species',
  value_table = list(tobacco = 1.0, soybean = Inf)
)

# Calculate Cc
licor_data <- apply_gm(licor_data)

# Calculate temperature-dependent values of C3 photosynthetic parameters
licor_data <- calculate_arrhenius(licor_data, c3_arrhenius_sharkey)

# The default optimizer uses randomness, so we will set a seed to ensure the
# results from this fit are always identical
set.seed(1234)

# Fit the C3 A-Ci curves
c3_aci_results <- consolidate(by(
  licor_data,                       # The `exdf` object containing the curves
  licor_data[, 'curve_identifier'], # A factor used to split `licor_data` into chunks
  fit_c3_aci,                       # The function to apply to each chunk of `licor_data`
  Ca_atmospheric = 420              # Additional argument passed to `fit_c3_aci`
))


# Plot the residuals
xyplot(
  A_residuals ~ Ci | curve_identifier,
  data = c3_aci_results$fits$main_data,
  type = 'b',
  pch = 16,
  grid = TRUE,
  xlab = paste0('Intercellular CO2 concentration (', c3_aci_results$fits$units$Ci, ')'),
  ylab = paste0('Assimilation rate residual (measured - fitted)\n(', c3_aci_results$fits$units$A, ')')
)

###
### SYNTHESIS:
### Using plots and statistics to help draw conclusions from the data
###

# View values of J from each fit
c3_aci_results$parameters[, c('curve_identifier', 'J_at_25_lower', 'J_at_25', 'J_at_25_upper')]

# View values of Vcmax from each fit
c3_aci_results$parameters[, c('curve_identifier', 'Vcmax_at_25_lower', 'Vcmax_at_25', 'Vcmax_at_25_upper')]

# Make a barchart showing average Vcmax values
barchart_with_errorbars(
  c3_aci_results$parameters[, 'Vcmax_at_25'],
  c3_aci_results$parameters[, 'species'],
  ylim = c(0, 180),
  xlab = 'Species',
  ylab = paste0('Vcmax at 25 degrees C (', c3_aci_results$parameters$units$Vcmax_at_25, ')')
)

# Make a boxplot showing the distribution of Vcmax values
bwplot(
  Vcmax_at_25 ~ species,
  data = c3_aci_results$parameters$main_data,
  ylim = c(0, 180),
  xlab = 'Species',
  ylab = paste0('Vcmax at 25 degrees C (', c3_aci_results$parameters$units$Vcmax_at_25, ')')
)

# Compute the average and standard error of each parameter for each species
c3_aci_averages <- basic_stats(c3_aci_results$parameters, 'species')

# View the averages and errors
columns_to_view <- c(
  'species',
  'Vcmax_at_25_avg', 'Vcmax_at_25_stderr',
  'J_at_25_avg', 'J_at_25_stderr',
  'RL_at_25_avg', 'RL_at_25_stderr',
  'Tp_avg', 'Tp_stderr'
)

c3_aci_averages[ , columns_to_view]

References

Caemmerer, S. von. 2000. Biochemical Models of Leaf Photosynthesis. CSIRO Publishing. https://doi.org/10.1071/9780643103405.

Lochocki, Edward B., and Justin M. McGrath. 2024. “Widely Used Variants of the Farquhar-von-Caemmerer-Berry Model Can Cause Errors in Parameter Estimation and Simulations.” Under Review.

Sharkey, Thomas D., Carl J. Bernacchi, Graham D. Farquhar, and Eric L. Singsaas. 2007. “Fitting Photosynthetic Carbon Dioxide Response Curves for C3 Leaves.” Plant, Cell & Environment 30 (9): 1035–40. https://doi.org/10.1111/j.1365-3040.2007.01710.x.