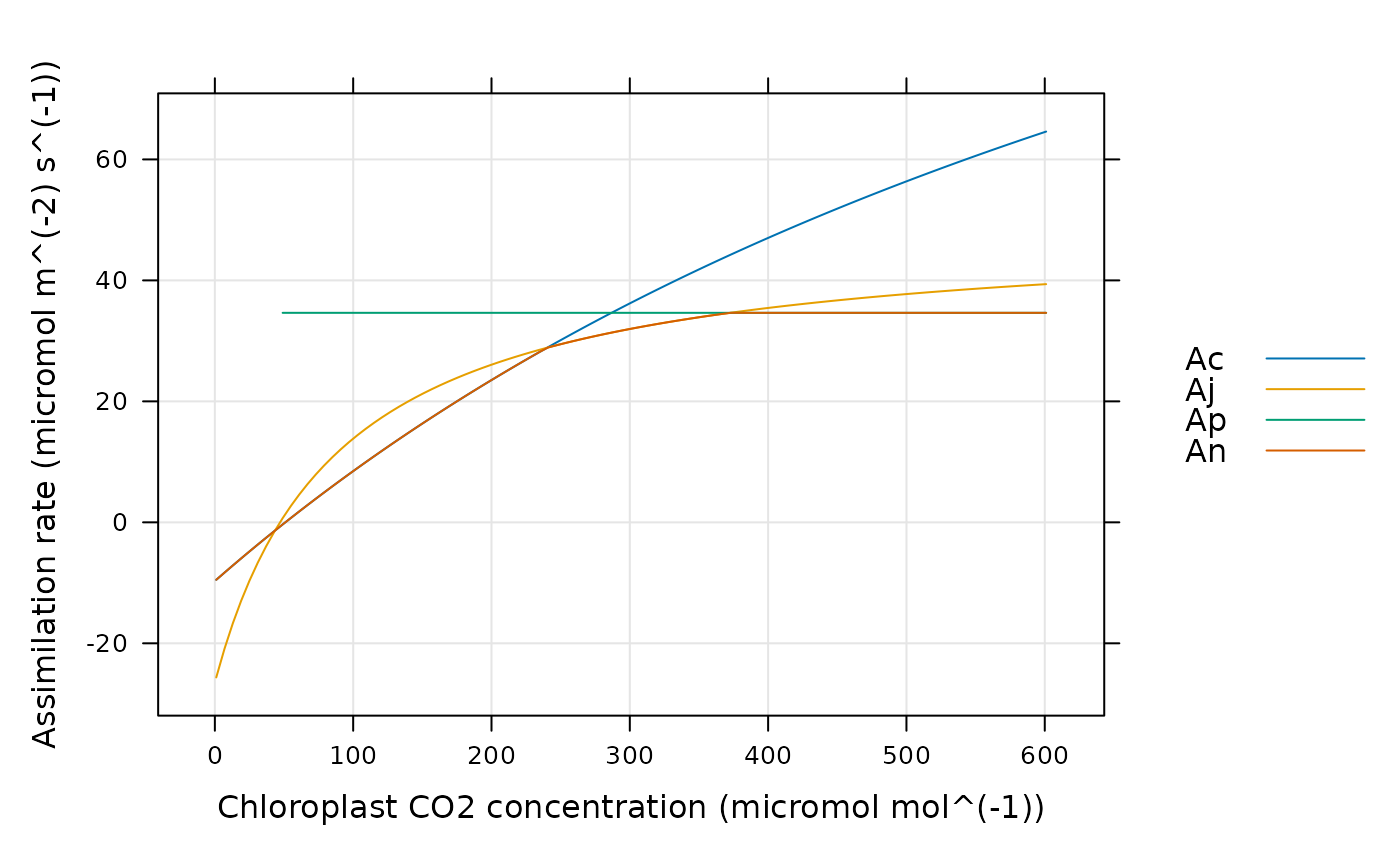Skip to contents padding-top: 70px;

Calculate C3 assimilation rates

calculate_c3_assimilation.Rd

Calculates C3 assimilation rates based on the Farquhar-von-Caemmerer-Berry model. This function can accomodate alternative colum names for the variables taken from Licor files in case they change at some point in the future. This function also checks the units of each required column and will produce an error if any units are incorrect.

Usage

calculate_c3_assimilation(
    exdf_obj,
    alpha_g,
    alpha_old,
    alpha_s,
    alpha_t,
    Gamma_star,
    J_at_25,
    RL_at_25,
    Tp_at_25,
    Vcmax_at_25,
    atp_use = 4.0,
    nadph_use = 8.0,
    curvature_cj = 1.0,
    curvature_cjp = 1.0,
    cc_column_name = 'Cc',
    j_norm_column_name = 'J_norm',
    kc_column_name = 'Kc',
    ko_column_name = 'Ko',
    oxygen_column_name = 'oxygen',
    rl_norm_column_name = 'RL_norm',
    total_pressure_column_name = 'total_pressure',
    tp_norm_column_name = 'Tp_norm',
    vcmax_norm_column_name = 'Vcmax_norm',
    hard_constraints = 0,
    perform_checks = TRUE,
    return_exdf = TRUE,
    ...
  )

Arguments

exdf_obj

An exdf object.

alpha_g

A dimensionless parameter where 0 <= alpha_g <= 1, representing the proportion of glycolate carbon taken out of the photorespiratory pathway as glycine. alpha_g is often assumed to be 0. If alpha_g is not a number, then there must be a column in exdf_obj called alpha_g with appropriate units. A numeric value supplied here will overwrite the values in the alpha_g column of exdf_obj if it exists.

alpha_old

A dimensionless parameter where 0 <= alpha_old <= 1, representing the fraction of remaining glycolate carbon not returned to the chloroplast after accounting for carbon released as CO2. alpha_old is often assumed to be 0. If alpha_old is not a number, then there must be a column in exdf_obj called alpha_old with appropriate units. A numeric value supplied here will overwrite the values in the alpha_old column of exdf_obj if it exists.

alpha_s

A dimensionless parameter where 0 <= alpha_s <= 0.75 * (1 - alpha_g) representing the proportion of glycolate carbon taken out of the photorespiratory pathway as serine. alpha_s is often assumed to be 0. If alpha_s is not a number, then there must be a column in exdf_obj called alpha_s with appropriate units. A numeric value supplied here will overwrite the values in the alpha_s column of exdf_obj if it exists.

alpha_t

A dimensionless parameter where 0 <= alpha_t <= 1 representing the proportion of glycolate carbon taken out of the photorespiratory pathway as CH2-THF. alpha_t is often assumed to be 0. If alpha_t is not a number, then there must be a column in exdf_obj called alpha_t with appropriate units. A numeric value supplied here will overwrite the values in the alpha_t column of exdf_obj if it exists.

Gamma_star

The CO2 compensation point in the absence of day respiration, expressed in micromol mol^(-1). If Gamma_star is not a number, then there must be a column in exdf_obj called Gamma_star with appropriate units. A numeric value supplied here will overwrite the values in the Gamma_star column of exdf_obj if it exists.

J_at_25

The electron transport rate at 25 degrees C, expressed in micromol m^(-2) s^(-1). Note that this is _not_ Jmax, and in general will depend on the incident photosynthetically active flux density. If J_at_25 is not a number, then there must be a column in exdf_obj called J_at_25 with appropriate units. A numeric value supplied here will overwrite the values in the J_at_25 column of exdf_obj if it exists.

RL_at_25

The respiration rate at 25 degrees C, expressed in micromol m^(-2) s^(-1). If RL_at_25 is not a number, then there must be a column in exdf_obj called RL_at_25 with appropriate units. A numeric value supplied here will overwrite the values in the RL_at_25 column of exdf_obj if it exists.

Tp_at_25

The maximum rate of triphosphate utilization at 25 degrees C, expressed in micromol m^(-2) s^(-1). If Tp_at_25 is not a number, then there must be a column in exdf_obj called Tp_at_25 with appropriate units. A numeric value supplied here will overwrite the values in the Tp_at_25 column of exdf_obj if it exists.

Vcmax_at_25

The maximum rate of rubisco carboxylation at 25 degrees C, expressed in micromol m^(-2) s^(-1). If Vcmax_at_25 is not a number, then there must be a column in exdf_obj called Vcmax_at_25 with appropriate units. A numeric value supplied here will overwrite the values in the Vcmax_at_25 column of exdf_obj if it exists.

atp_use

The number of ATP molecules used per C3 cycle.

nadph_use

The number of NADPH molecules used per C3 cycle.

curvature_cj

A dimensionless quadratic curvature parameter greater than or equal to 0 and less than or equal to 1 that sets the degree of co-limitation between Wc and Wj. A value of 1 indicates no co-limitation.

curvature_cjp

A dimensionless quadratic curvature parameter greater than or equal to 0 and less than or equal to 1 that sets the degree of co-limitation between Wcj and Wp. A value of 1 indicates no co-limitation.

cc_column_name

The name of the column in exdf_obj that contains the chloroplastic CO2 concentration in micromol mol^(-1).

j_norm_column_name

The name of the column in exdf_obj that contains the normalized J values (with units of normalized to J at 25 degrees C).

kc_column_name

The name of the column in exdf_obj that contains the Michaelis-Menten constant for rubisco carboxylation in micromol mol^(-1).

ko_column_name

The name of the column in exdf_obj that contains the Michaelis-Menten constant for rubisco oxygenation in mmol mol^(-1).

oxygen_column_name

The name of the column in exdf_obj that contains the concentration of O2 in the ambient air, expressed as a percentage (commonly 21% or 2%); the units must be percent.

rl_norm_column_name

The name of the column in exdf_obj that contains the normalized RL values (with units of normalized to RL at 25 degrees C).

total_pressure_column_name

The name of the column in exdf_obj that contains the total pressure in bar.

tp_norm_column_name

The name of the column in exdf_obj that contains the normalized Tp values (with units of normalized to Tp at 25 degrees C).

vcmax_norm_column_name

The name of the column in exdf_obj that contains the normalized Vcmax values (with units of normalized to Vcmax at 25 degrees C).

hard_constraints

An integer numerical value indicating which types of hard constraints to place on the values of input parameters; see below for more details.

perform_checks

A logical value indicating whether to check units for the required columns. This should almost always be TRUE. The option to disable these checks is only intended to be used when fit_c3_aci calls this function, since performing these checks many times repeatedly slows down the fitting procedure.

return_exdf

A logical value indicating whether to return an exdf object. This should almost always be TRUE. The option to return a vector is mainly intended to be used when fit_c3_aci calls this function, since creating an exdf object to return will slow down the fitting procedure.

...

Optional arguments; see below.

Details

The Busch et al. (2018) and Busch (2020) model:

This function generally follows the Farquhar-von-Caemmerer-Berry model as described in Busch et al. (2018) and Busch (2020) with a few modifications described below. In this formulation, the steady-state net CO2 assimilation rate An is calculated according to

An = (1 - Gamma_star_agt / PCc) * Vc - RL,

where Gamma_star is the CO2 compensation point in the absence of day respiration, Gamma_star_agt is the effective value of Gamma_star accounting for glycolate carbon remaining in the cytosol, PCc is the partial pressure of CO2 in the chloroplast, Vc is the RuBP carboxylation rate, and RL is the rate of respiration in the light. Gamma_star_agt is given by

Gamma_star_agt = (1 - alpha_g + 2 * alpha_t) * Gamma_star,

where alpha_g and alpha_t are the fractions of glycolate carbon leaving the photorespiratory pathway as glycine and CH2-THF, respectively.

The model considers three potential values of Vc that correspond to limitations set by three different processes: Rubisco activity, RuBP regeneration, and triose phopsphate utilization (TPU). The Rubisco-limited carboxylation rate Wc is given by

Wc = PCc * Vcmax / (PCc + Kc * (1.0 + POc / Ko)),

where Vcmax is the maximum rate of Rubisco carboxylation, Kc is the Michaelis-Menten constant for CO2, Ko is the Michaelis-Menten constant for O2, and POc is the partial pressure of O2 in the chloroplast.

The RuBP-regeneration-limited carboxylation rate Wj is given by

Wj = PCc * J / (4 * PCc + Gamma_star_agt * (8 + 16 * alpha_g - 8 * alpha_t + 8 * alpha_s)),

where J is the RuBP regeneration rate and alpha_s is the fraction of glycolate carbon leaving the photorespiratory pathway as serine.

The TPU-limited carboxylation rate is given by

Wp = PCc * 3 * Tp / (PCc - Gamma_star_agt * (1 + 3 * alpha_g + 6 * alpha_t + 4 * alpha_s)),

where Tp is the maximum rate of triose phosphate utilization. Note that this equation only applies when PCc > Gamma_star_agt * (1 + 3 * alpha_g + 6 * alpha_t + 4 * alpha_s); for smaller values of PCc, TPU cannot limit the RuBP carboxylation rate and Wp = Inf. (Lochocki & McGrath, under review).

The actual carboxylation rate is typically chosen to be the smallest of the three potential rates:

Vc = min{Wc, Wj, Wp}.

However, it is also possible to allow co-limitation between the processes by using quadratic mixing equations. In other words, the carboxylation rate co-limitated by Rubisco activity and RuBP regeneration Wcj is given by the smaller root of the following quadratic equation:

curvature_cj * Wcj^2 - Wcj * (Wc + Wj) + Wc * Wj = 0,

where curvature_cj described the "curvature" of the mixing; if curvature_cj is 1, this is equivalent to Wcj = min{Wc, Wj}; if curvature_cj is 0, then Wcj is the geometric mean of Wc and Wj. Any value below 1 will produce a smooth curve rather than the abrupt transitions that occur when choosing the simple minimum. Likewise, the carboxylation rate co-limited by Wcj and Wp (called Wcjp; in other words, the rate co-limited by all three processes) is given by the smaller root of

curvature_cjp * Wcjp^2 - Wcjp * (Wcj + Wp) + Wcj * Wp = 0.

Then, Wcjp is used in place of Vc when calculating the net CO2 assimilation rate. For more information about the quadratic mixing technique, see Collatz et al. (1990) and Collatz et al. (1991).

In the equations above, several of the variables depend on the leaf temperature. In particular, the leaf-temperature-adjusted values of Vcmax, J, Tp, and RL are determined from their base values at 25 degrees C and a temperature-dependent multiplicative factor.

Also note that PCc is calculated from the chloroplastic CO2 concentration Cc using the total pressure (ambient pressure + chamber overpressure).

In addition to the carboxylation and assimilation rates already mentioned, it is also possible to calculate the net CO2 assimilation rates determined by Rubisco activity, RuBP regeneration, and TPU as follows:

Ac = (1 - Gamma_star_agt / PCc) * Wc - RL

Aj = (1 - Gamma_star_agt / PCc) * Wj - RL

Ap = (1 - Gamma_star_agt / PCc) * Wp - RL

The Busch model with nitrogen restrictions:

Note that the implementation as described above does not currently facilitate the inclusion of nitrogen limitations (Equations 15-21 in Busch et al. (2018)).

The "old" model:

In an older version of the model, alpha_g, alpha_s, and alpha_t are replaced with a single parameter alpha_old. Most publications refer to this simply as alpha, but here we follow the notation of Busch et al. (2018) for clarity. In this version, there is no disctinction between Gamma_star_agt and Gamma_star. Other differences are described below.

The RuBP-regeneration-limited carboxylation rate Wj is given by

Wj = PCc * J / (atp_use * PCc + nadph_use * Gamma_star),

Here we have allowed atp_use and nadph_use to be variables rather than taking fixed values (as they do in many sources). This is necessary because not all descriptions of the FvCB model use the same values, where the different values are due to different assumptions about the energy requirements of RuBP regeneration.

The TPU-limited carboxylation rate is given by

Wp = PCc * 3 * Tp / (PCc - Gamma_star * (1 + 3 * alpha_old)),

Note that this equation only applies when PCc > Gamma_star * (1 + 3 * alpha_old); for smaller values of PCc, TPU cannot limit the RuBP carboxylation rate and Wp = Inf. (Lochocki & McGrath, under review).

Using either version of the model:

When using calculate_c3_assimilation, it is possible to use either version of the model. Setting alpha_g, alpha_s, and alpha_t to zero is equivalent to using the older version of the model, while setting alpha_old = 0 is equivalent to using the newer version of the model. If all alpha parameters are zero, there is effectively no difference between the two versions of the model. Attempting to set a nonzero alpha_old if either alpha_g, alpha_s, or alpha_t is nonzero is forbidden since it would represent a mix between the two models; if such values are passed as inputs, then an error will be thrown.

Hard constraints:

Most input parameters to the FvCB model have hard constraints on their values which are set by their biochemical or physical interpretation; for example, Vcmax cannot be negative and alpha_g must lie between 0 and 1. Yet, because of measurement noise, sometimes it is necessary to use values outside these ranges when fitting an A-Ci curve with fit_c3_aci or fit_c3_variable_j. To accomodate different potential use cases, it is possible to selectively apply these hard constraints by specifying different values of the hard_constraints input argument:

  • hard_constraints = 0: Constraints are only placed on inputs that are user-supplied and cannot be fit, such as Kc.

  • hard_constraints = 1: Includes the same constraints as when hard_constraints is 0, with the additional constraint that all Cc values must be non-negative.

  • hard_constraints = 2: Includes the same constraints as when hard_constraints is 1, which additional constraints on the parameters that can be fitted. For example, Vcmax_at_25 must be non-negative and alpha_g must lie between 0 and 1.

If any input values violate any of the specified constraints, an error message will be thrown.

Optional arguments:

  • use_min_A: If an input argument called use_min_A is supplied and its value is TRUE, then the "minimum assimilation" variant of the FvCB model will be used. In this case, An will be calculated as An = min{Ac, Aj, Ap}. In general, using this variant is not recommended.It should only be used to investigate errors that may occur when using the minimal assimilation rate rather than the minimal carboxylation rate.

  • TPU_threshold: If an input argument called TPU_threshold is supplied and its numeric value is not NULL, then TPU limitations will only be allowed for values of Cc above this threshold. This threshold will be used in place of the values discussed in the equations above. In general, using this option is not recommended. It should only be used to investigate errors that may occur when using a fixed TPU threshold.

  • use_FRL: If an input argument called use_FRL is supplied and its value is TRUE, then An will always be set to Ac for Cc < Gamma_star. This "forced Rubisco limitation" can only be used along with the "minimum assimilation" variant (use_min_A = TRUE).

  • consider_depletion: If an input argument called consider_depletion is supplied and its value is TRUE, then RuBP depletion will be considered to be an additional potential limiting process. In this case, Vc will be calculated as Vc = min{Wc, Wj, Wp, Wd}, where Wd is zero when Cc < Gamma_star and Inf otherwise. Note that the value of Wd (and Ad = (1 - Gamma_star / PCc) * Wd - RL) will always be returned, regardless of whether RuBP depletion is considered when calculating An.

References:

  • Busch, Sage, & Farquhar, G. D. "Plants increase CO2 uptake by assimilating nitrogen via the photorespiratory pathway." Nature Plants 4, 46–54 (2018) [doi:10.1038/s41477-017-0065-x ].

  • Busch "Photorespiration in the context of Rubisco biochemistry, CO2 diffusion and metabolism." The Plant Journal 101, 919–939 (2020) [doi:10.1111/tpj.14674 ].

  • von Caemmerer, S. "Biochemical Models of Leaf Photosynthesis" (CSIRO Publishing, 2000) [doi:10.1071/9780643103405 ].

  • Collatz, G. J., Ball, J. T., Grivet, C. & Berry, J. A. "Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: a model that includes a laminar boundary layer." Agricultural and Forest Meteorology 54, 107–136 (1991) [doi:10.1016/0168-1923(91)90002-8 ].

  • Collatz, G. J., Berry, J. A., Farquhar, G. D. & Pierce, J. "The relationship between the Rubisco reaction mechanism and models of photosynthesis." Plant, Cell & Environment 13, 219–225 (1990) [doi:10.1111/j.1365-3040.1990.tb01306.x ].

  • Lochocki & McGrath "Widely Used Variants of the Farquhar-von-Caemmerer-Berry Model Can Cause Errors in Parameter Estimates and Simulations." submitted.

Value

The return value depends on the value of return_exdf:

  • If return_exdf is TRUE, the return value is an exdf object with the following columns, calculated as described above: Tp_tl, Vcmax_tl, RL_tl, J_tl, Ac, Aj, Ap, An, Vc, and others. The category for each of these new columns is calculate_c3_assimilation to indicate that they were created using this function.

  • If return_exdf is FALSE, the return value is a list with the following named elements: An, Ac, Aj, Ap, and J_tl. Each element is a numeric vector.

Examples

# Simulate a C3 A-Cc curve with specified leaf temperature and photosynthetic
# parameters and plot the net assimilation rate along with the different
# enzyme-limited rates
inputs <- exdf(data.frame(
  Cc = seq(1, 601, by = 6),
  Tleaf = 30,
  total_pressure = 1,
  oxygen = 21
))

inputs <- document_variables(
  inputs,
  c('', 'Cc',             'micromol mol^(-1)'),
  c('', 'Tleaf',          'degrees C'),
  c('', 'total_pressure', 'bar'),
  c('', 'oxygen',         'percent')
)

inputs <- calculate_temperature_response(inputs, c3_temperature_param_sharkey, 'Tleaf')

assim <- calculate_c3_assimilation(inputs, 0, 0, 0, 0, '', 150, 1, 12, 120)

lattice::xyplot(
  Ac + Aj + Ap + An ~ Cc,
  data = cbind(inputs, assim)$main_data,
  type = 'l',
  grid = TRUE,
  auto = TRUE,
  xlab = paste0('Chloroplast CO2 concentration (', inputs$units$Cc, ')'),
  ylab = paste0('Assimilation rate (', assim$units$An, ')')
)