Calculate C4 assimilation rates using a hyperbola — calculate_c4_assimilation

Calculates C4 assimilation rates based on an empirical hyperbolic model. This function can accomodate alternative colum names for the variables taken from Licor files in case they change at some point in the future. This function also checks the units of each required column and will produce an error if any units are incorrect.

Usage

calculate_c4_assimilation_hyperbola(
    exdf_obj,
    c4_curvature,
    c4_slope,
    rL,
    Vmax,
    ci_column_name = 'Ci',
    hard_constraints = 0,
    perform_checks = TRUE,
    return_exdf = TRUE
  )

Arguments

exdf_obj: An exdf object.
c4_curvature: The empirical curvature parameter of the hyperbola (dimensionless). If c4_curvature is not a number, then there must be a column in exdf_obj called c4_curvature with appropriate units. A numeric value supplied here will overwrite the values in the c4_curvature column of exdf_obj if it exists.
c4_slope: The empirical slope parameter of the hyperbola (mol m^(-2) s^(-1)). If c4_slope is not a number, then there must be a column in exdf_obj called c4_slope with appropriate units. A numeric value supplied here will overwrite the values in the c4_slope column of exdf_obj if it exists.
rL: The respiration rate, expressed in micromol m^(-2) s^(-1). If rL is not a number, then there must be a column in exdf_obj called rL with appropriate units. A numeric value supplied here will overwrite the values in the rL column of exdf_obj if it exists.
Vmax: The maximum gross assimilation rate, expressed in micromol m^(-2) s^(-1). If Vmax is not a number, then there must be a column in exdf_obj called Vmax with appropriate units. A numeric value supplied here will overwrite the values in the Vmax column of exdf_obj if it exists.
ci_column_name: The name of the column in exdf_obj that contains the intercellular CO2 concentration, expressed in micromol mol^(-1).
hard_constraints: An integer numerical value indicating which types of hard constraints to place on the values of input parameters; see below for more details.
perform_checks: A logical value indicating whether to check units for the required columns. This should almost always be TRUE. The option to disable these checks is only intended to be used when fit_c4_aci_hyperbola calls this function, since performing these checks many times repeatedly slows down the fitting procedure.
return_exdf: A logical value indicating whether to return an exdf object. This should almost always be TRUE. The option to return a vector is mainly intended to be used when fit_c4_aci_hyperbola calls this function, since creating an exdf object to return will slow down the fitting procedure.

Details

General Description of the Model

In contrast to the mechanistic model implemented in calculate_c4_assimilation, this is a simple empirical model for C4 assimilation based on a four-parameter hyperbola. In this model, the net CO2 assimilation rate (An) is given by

An = Ag - rL,

where Ag is the gross assimilation rate and rL is the respiration rate. In turn, Ag is given by the smaller root of the following quadratic equation:

curvature * Ag^2 - (Vinitial + Vmax) * Ag + Vinitial * Vmax = 0,

where 0 <= curvature <= 1 is an empirical curvature factor, Vmax is the maximum gross assimilation rate, and Vinitial represents the initial response of Ag to increases in the intercellular CO2 concentration (Ci):

Vinitial = slope * Ci.

Here the slope is another empirical factor.

By including the respiration offset, it is also possible to define two other quantities: the maximum net CO2 assimilation rate (Amax) and the initial net CO2 assimilation rate (Ainitial). These are given by

Amax = Vmax - rL

and

Ainitial = Vinitial - rL.

Overall, this model exhibits a linear response of An to Ci at low Ci, a flat plateau of An at high Ci, and a smooth transition between these regions. The sharpess of the transition is set by the curvature. When curvature = 1, the model simplifies to

An = min{Vinitial, Vmax} - rL = min{Ainitial, Amax}.

As the curvature increases to 1, the transition becomes smoother. When the curvature is not zero, An approaches Amax asymptotically, and may not reach Amax at a reasonable value of Ci.

Code implementation

In this function, curvature and slope above are referred to as c4_curvature and c4_slope to avoid any potential ambiguity with other models that may also have curvature and slope parameters.

Temperature response

Because this model does not represent any photosynthetic mechanisms, temperature response functions are not applied.

Hard constraints

Most input parameters to the this model have hard constraints on their values which are set by their interpretation; for example, Vmax cannot be negative and c4_curvature must lie between 0 and 1. Yet, because of measurement noise, sometimes it is necessary to use values outside these ranges when fitting an A-Ci curve with fit_c4_aci_hyperbola. To accomodate different potential use cases, it is possible to selectively apply these hard constraints by specifying different values of the hard_constraints input argument:

hard_constraints = 0: No constraints are applied.
hard_constraints = 1: Checks whether all Ci values are non-negative.
hard_constraints = 2: Includes the same constraints as when hard_constraints is 1, which additional constraints on the parameters that can be fitted. For example, Vmax must be non-negative and c4_curvature must lie between 0 and 1.

If any input values violate any of the specified constraints, an error message will be thrown.

Value

The return value depends on the value of return_exdf:

If return_exdf is TRUE, the return value is an exdf object with the following columns: Ag, Ainitial, Amax, An, c4_curvature, c4_slope, rL, Vinitial, Vmax, and c4_assimilation_hyperbola_msg. Most of these are calculated as described above, while several are copies of the input arguments with the same name. The c4_assimilation_hyperbola_msg is usually blank but may contain information about any issues with the inputs. The category for each of these new columns is calculate_c4_assimilation_hyperbola to indicate that they were created using this function.
If return_exdf is FALSE, the return value is a numeric vector containing the calculated values of An.

Examples

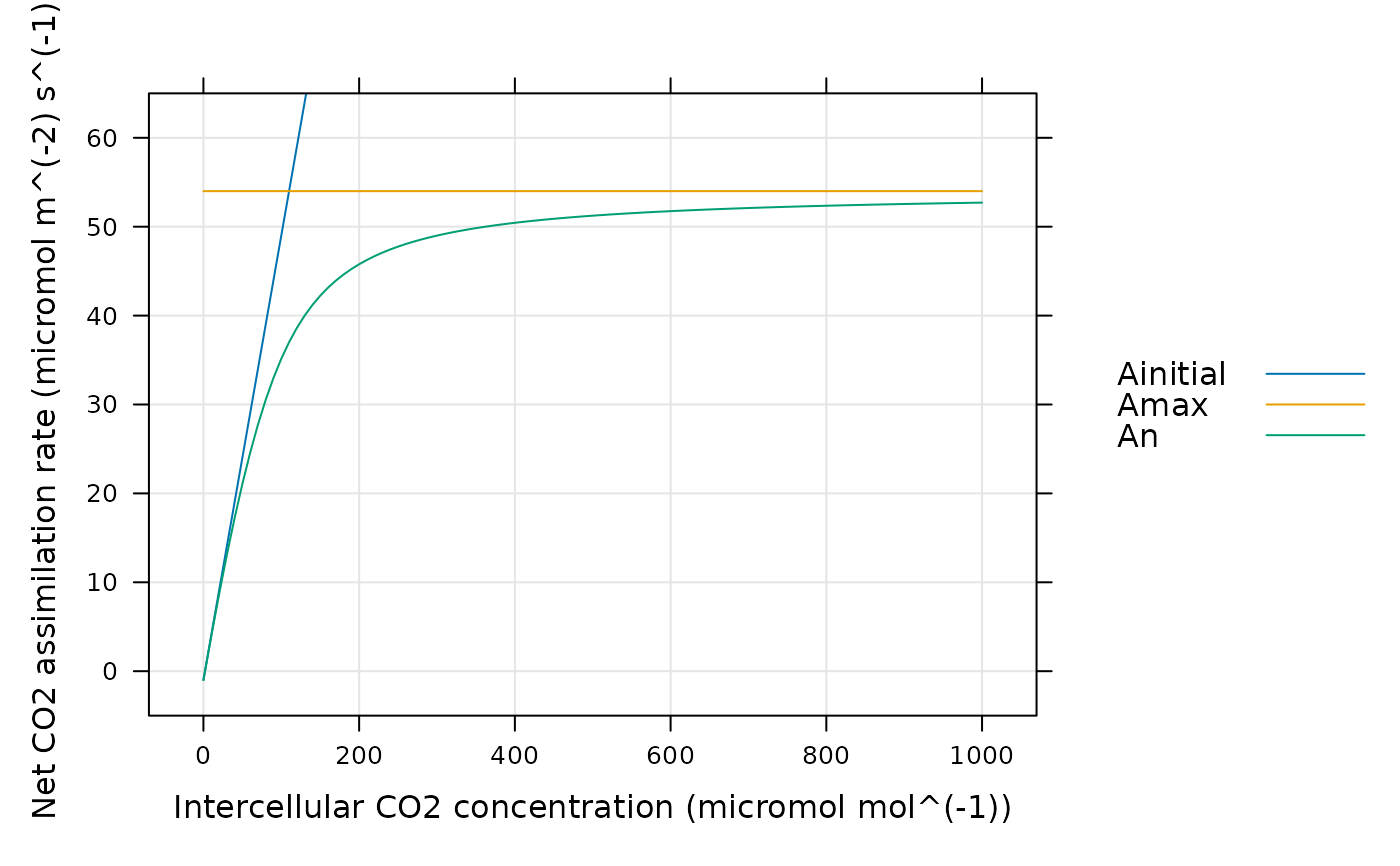
# Simulate a C4 A-Ci curve and plot the net assimilation rate.
npts <- 101

inputs <- exdf(data.frame(
  Ci = seq(0, 1000, length.out = npts),
  total_pressure = 1
))

inputs <- document_variables(
  inputs,
  c('', 'Ci',             'micromol mol^(-1)'),
  c('', 'total_pressure', 'bar')
)

assim <- calculate_c4_assimilation_hyperbola(inputs, 0.8, 0.5, 1.0, 55)

lattice::xyplot(
  Ainitial + Amax + An ~ inputs[, 'Ci'],
  data = assim$main_data,
  type = 'l',
  grid = TRUE,
  auto = TRUE,
  ylim = c(-5, 65),
  xlab = paste0('Intercellular CO2 concentration (', inputs$units$Ci, ')'),
  ylab = paste0('Net CO2 assimilation rate (', assim$units$An, ')')
)